Catégorie de navigation
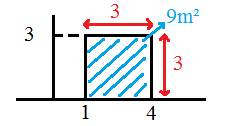
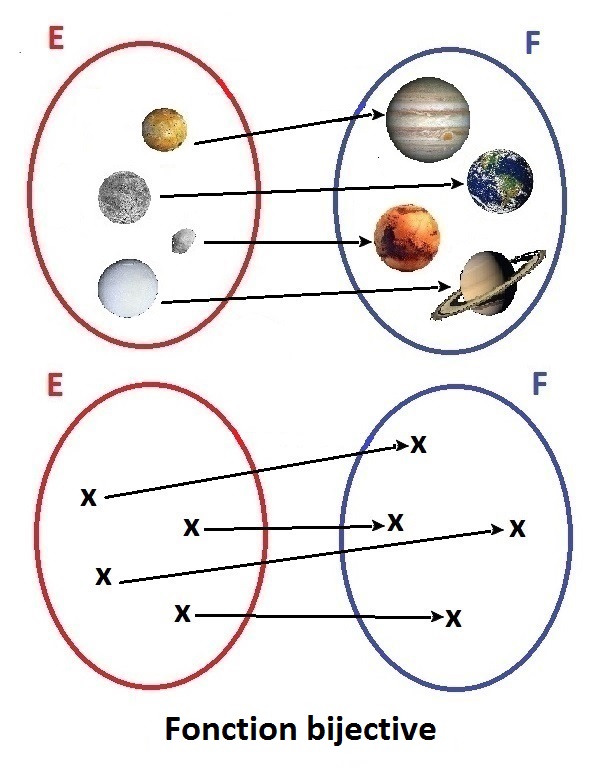
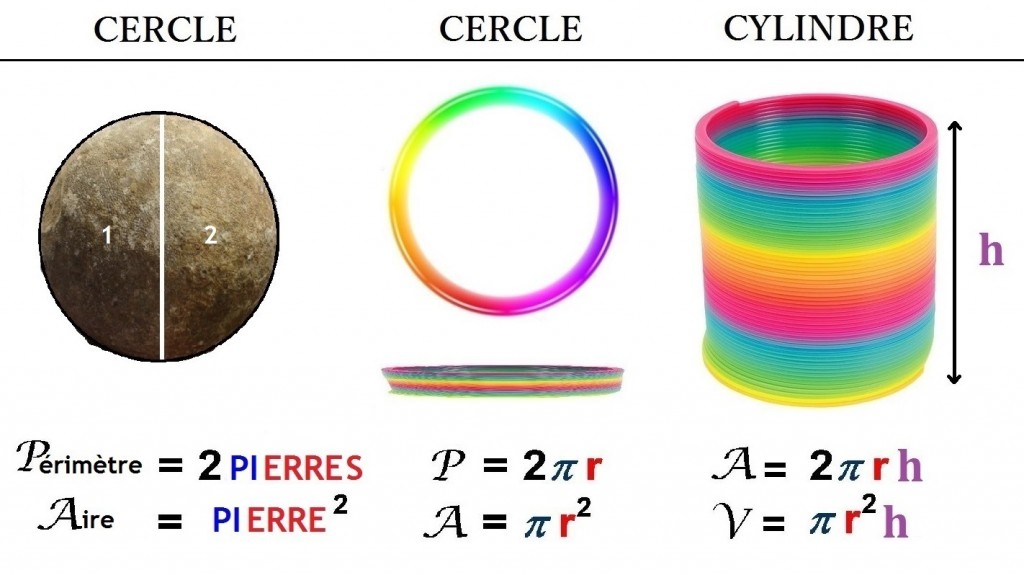
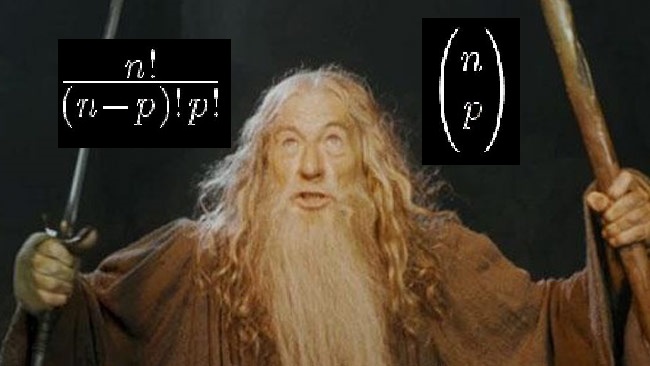Mathématiques
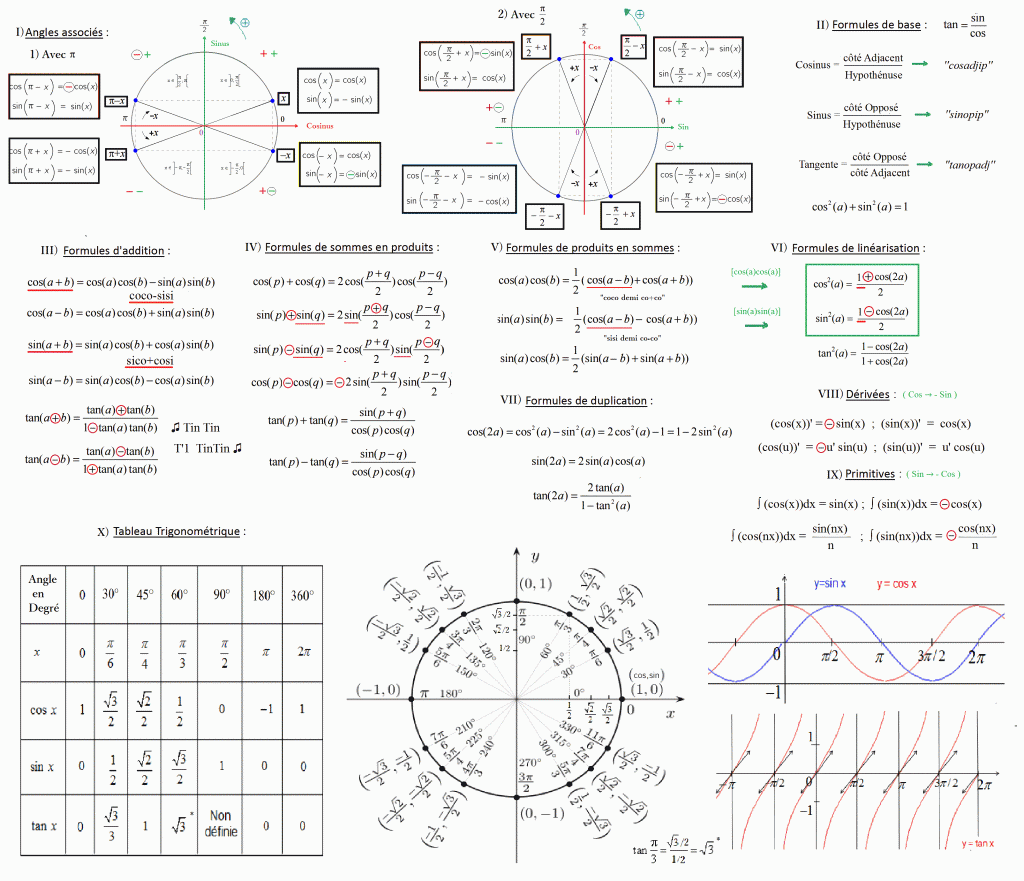
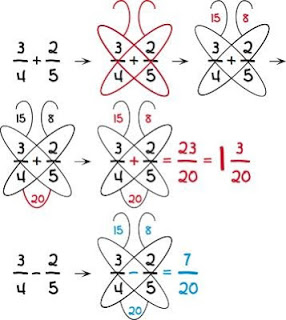
Vous trouverez ici tous les moyens mnémotechniques en mathématiques, géométrie, trigonométrie, algèbre, ainsi que toute une série d’outils pour réaliser des multiplications et des calculs plus facilement. Des exercices illustrés permettant d’améliorer vos compétences et d’appréhender cette discipline avec sérénité.
Les Formules Géométriques (Cercle, Cylindre, Sphère)
Si avant de lire cet article vous ne vous souvenez plus de vos formules géométriques, voici 3 astuces qui vous permettront de ne plus jamais les oublier, notamment pour le cercle, le cylindre, et la sphère ! (Nous vous conseillons de vous…
Les formules de trigonométrie, facile!
La trigonométrie, c'est l'une des bases fondamentales qu'il faut maîtriser en maths, elle est partout ! Cependant, les formules de trigo ne sont pas si faciles à mémoriser (certes on peut les retrouver grâce à des démonstrations…
Hyperboloïde à 1 ou 2 nappes ?
Une équation de quadrique de la forme x²/a² + y²/b² - z²/c² = ±1 correspond à l'équation d'un hyperboloïde... mais est-ce un hyperboloïde à une nappe ou bien à deux nappes ? Il suffit de compter le nombre de signes moins (-) dans…
Double produit vectoriel et bac à sable
Il arrive souvent au détour de calculs mathématiques ou physiques qu'on note l'apparition d'un double produit vectoriel à calculer... et c'est souvent le drame ! Pour ne plus hésiter, on peut simplement retenir la locution : Bac à sable.…
Retenir les unités de mesure (longueur, masse et volume) et l’ordre des multiples et sous…
Afin de retenir cet ordre, apprenez ces trois phrases. La longueur comme unité de mesure (L'unité de mesure des longueurs est le mètre, ses multiples et sous-multiples) (km hm dam) m (dm cm mm) = (Multiples) m (Sous multiples) …
Bernoulli et sa prononciation
Pour ne pas écorcher le nom du mathématico-physicien (ou physico-mathématicien ?) Daniel Bernoulli, retenez que : Bernoulli n'était pas une nouille ! Bernoulli n'était pas une nouille ! Répétez ! Répétez ! Donc plus de…
Comment créer des codes secrets inviolables avec la cryptographie
LE CODE KYD LE CODE KYD 1.1 (Inventé à titre pédagogique pour jeretiens.net) Paradoxalement parlant "l'avant propos" de cet article sera placé en bas de page, à lire cependant avant de commencer si toutefois vous ne connaissez rien…
Addition et soustraction de fractions, facile !
"On ne mélange pas les pommes et les poires" nous ont répété sans relâche nos instituteurs. La théorie de cette opération veut que l'on trouve le dénominateur commun. La façon la plus simple de faire cela est de multiplier les…
Les fonctions et leurs dessins
La fonction est le résultat d'opérations mathématiques à partir d'une variable. La fonction s'exprime par une courbe du plan qui la représente. Voici une manière amusante, grâce à un mnémonique visuel, pour retenir les courbes des…
Racine carrée de 3 = 1,732 – Date de la bataille de Poitiers
La racine carrée de 3 vaut 1,732. Pour retenir la valeur de la racine carrée de 3, il suffit de se rappeler quand la Bataille de Poitiers a eu lieu: en 732. Plus précisément: "En" (pour 1), 732: 1,732. Sans rentrer dans les…