Si les trois mots du titre vous sont inconnus et semblent étranges.. c’est normal !
Ce sont des notions mathématiques assez abstraites, à la base même de l’algèbre.. mais pas de panique ! Cet article est là pour vous proposer des explications de ces notions, ainsi que des astuces mnémotechniques pour ne pas (ou plus) les confondre !
Tout d’abord, on va rapidement définir les symboles mathématiques, puis les utiliser pour comprendre le langage des mathématiciens !
On commence par ce qu’on appelle des quantificateurs, constamment utilisés en maths :
– Le symbole ∈ signifie ‘appartient’, par exemple une planète comme la Terre (l’élément) appartient au système Solaire (l’ensemble), soit planète ∈ système solaire, en maths on préfère remplacer la planète par un x et le système solaire par un ensemble E, on a donc x∈E (x appartient à E).
– Le symbole ∀ signifie ‘pour tout’, ‘quelque soit’, ‘n’importe lequel’, par exemple quelque soit la planète x appartenant au système solaire E se dit : ∀x ∈ E.
– Le symbole ∃ signifie ‘il existe’, par exemple il existe x planètes telluriques (rocheuses) dans le système solaire E se dit : ∃x∈E.
– Le symbole ⇔ signifie ‘équivalent’, ‘si et seulement si (ssi)’, pour avoir une équivalence (⇔) il faut à la fois une implication (⇒) et une réciproque (⇐), par exemple :
Implication (⇒) : « S’il y a du feu, alors il y a de la fumée. »
Réciproque (⇐) : « S’il y a de la fumée alors il y a du feu. »
Si les deux conditions (⇐et⇒) sont vérifiées, alors il y a équivalence (⇔) !
Normalement, tous les symboles concernant cet article ont été définis (bien sûr il y en a beaucoup d’autres en maths). Nous allons donc passer aux injections, aux surjections et puis aux bijections. Et pour mieux comprendre, nous utiliserons l’exemple des planètes et de leurs satellites !
Pour les trois notions, on prend E l’ensemble de départ (celui des satellites) et F l’ensemble d’arrivée (celui des planètes).
Injection :
On dit qu’une fonction est injective si tout élément de son espace d’arrivée possède au plus un antécédent par la fonction. Ainsi, pour une injection, un élément de F ne pourra jamais avoir plus d’un antécédent, le maximum d’antécédent est un.
Voici quelques schémas (des patatoïdes) pour mieux visualiser :
La Lune (satellites : ensemble E) est l’antécédent de la Terre (planètes : ensemble F), de même la Terre est l’image de la Lune.
Phobos est l’antécédent de Mars, de même Mars est l’image de Phobos.
Io est l’antécédent de Jupiter, de même Jupiter est l’image de Io.
Encelade est l’antécédent de Saturne, de même Saturne est l’image d’Encelade.
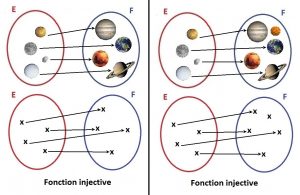
On peut remarquer que dans le cas de l’injectivité, une flèche au plus (au maximum) atteint les points de l’ensemble d’arrivé F.
Définition mathématique de l’injection : « Soient E et F deux ensembles quelconques et f une application de E dans F. f est injective si et seulement si tout élément y de F possède au plus un antécédent par f. »
– Mathématiquement parlant, on dit qu’une fonction f : E→F est injective ssi :
∀(x,y) ∈ E², f(x) = f(y) ⇒ x = y
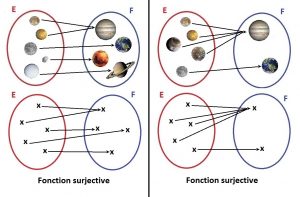
On peut remarquer que dans le cas de la surjectivité, tous les points de F sont atteints par au moins une flèche (ou plus) venant de E, alors que dans le cas où F n’est pas surjective, ce n’est pas vrai.
Définition mathématique de la surjection : « Soient E et F deux ensembles quelconques et f une application de E dans F. f est surjective si et seulement si tout élément y de F possède au moins un antécédent par f. »
– Mathématiquement parlant, on dit qu’une fonction f : E→F est surjective ssi :
∀ y ∈ F, ∃x ∈ E, f(x) = y
– En français : Une fonction f allant de E dans F (f : E→F) est surjective si et seulement si : pour tout élément y (∀y) appartenant à F (∈F), il existe un élément x de E (∃x∈E) tel qu’on puisse écrire f(x)=y. (Astuce en fin d’article)
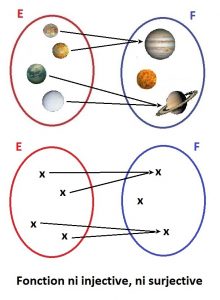
Ni injection, Ni surjection :
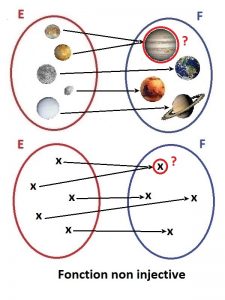
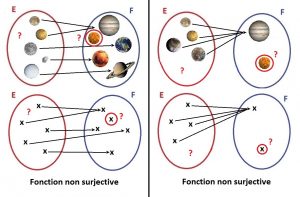
Comme on peut le constater, les satellites Io et Europe sont les deux antécédents de Jupiter ; Encelade et Titan sont les deux antécédents de Saturne (planète avec les anneaux) ; Vénus ne possède pas de satellite, donc pas d’antécédent ; ainsi aucune des propriétés ne sont respectées, il n’y a pas d’injection car il y a plus d’un antécédent pour Jupiter et Saturne, et il n’y a pas de surjection car la planète Vénus n’a pas d’antécédent (alors qu’il en faudrait au moins un).
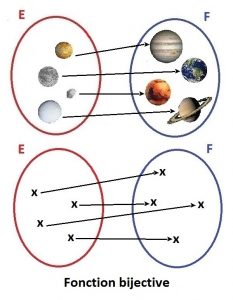
Bijection (injection et surjection) :
On dit qu’une fonction est bijective si tout élément de son espace d’arrivée possède exactement un antécédent par la fonction. Ainsi une fonction bijective est injective ET surjective, elle est bijective (si et seulement si) ssi elle admet un seul et unique antécédent, ni plus, ni moins !
On remarque qu’il y alors autant d’éléments dans E que dans F, en effet chaque image possède un seule et unique antécédent.
Définition mathématique de la bijection : « Soient E et F deux ensembles quelconques et f une application de E dans F. f est bijective si et seulement si tout élément y de F possède un unique antécédent par f. »
– Mathématiquement parlant, on dit qu’une fonction f : E→F est bijective ssi :
( à la suite du « ∃ » (« il existe »), il y a un point d’exclamation (!), ce qui modifie le sens de la phrase mathématique en « il existe un unique x » « ∃!x » )
– En français : Une fonction f allant de E dans F (f : E→F) est bijective si et seulement si pour tout élément y (∀y) appartenant à F (∈F), il existe un unique élément x de E (∃!x∈E) tel qu’on puisse écrire f(x)=y.
Astuces :
Dans cet article, nous avons donc vu qu’une fonction injective admettait au plus un antécédent, que la fonction surjective admettait au moins un antécédent, et qu’une fonction bijective admettait un seul et unique antécédent !
- Pour ne plus jamais se tromper en terme de vocabulaire entre injectif et surjectif, voici l’astuce :
Pour l’injection, il faut se dire que le médecin nous injecte au plus (au maximum) une dose de vaccin (contenant un virus atténué, suffisant pour induire l’immunité).
Pour la surjection, il faut se dire que lors d’un don du sang, le médecin nous en prélève, puis en introduit en grande quantité dans une poche, ainsi il «surjecte» au moins 300 mL de notre sang dans une poche.
- Une autre astuce est possible, mais moins orthodoxe.. la voici quand même.. :
Pour l’injection, il faut se dire qu’on s’injecte au plus (au maximum) une faible quantité de morphine.. juste assez pour se sentir mieux et ne pas tomber dans les pommes.. donc l’injection correspond à un antécédent au maximum.
Pour la surjection, il faut se dire qu’on se «surjecte» une grande quantité d’eau pour faire disparaître les effets.. donc la surjection correspond à au moins un antécédent.
Remarque mathématique :Un élément de l’ensemble de définition de f admet forcément une image par f. On a donc forcément une flèche partant de chaque point de l’ensemble de départ E, pour arriver sur un autre point de l’ensemble d’arrivée.
Remarque astronomique : Mercure et Vénus ne possèdent pas de satellites car ce sont les planètes les plus proches du Soleil, ainsi la gravité du Soleil est trop perturbante pour permettre à d’éventuels satellites de rester en orbite. Ainsi, dans les exemples précédents, Vénus ne possède pas de satellite.
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
- L’alphabet Arabe : les 28 lettres - 18 mars 2025
- Quelle est la différence entre Jaguar, Léopard et Guépard ? - 18 mars 2025

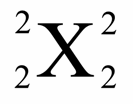
Ping : FJ Mathématiques Lycée (jadotf) | Pearltrees
Bonjour,
Cet article sur les injections, surjections, bijections comporte une petite erreur. Je me permets de vous la signaler si vous le voulez bien.
Veuillez, s’il vous plait, relire à partir de la 28ème ligne (INJECTION) jusqu’à la 31ème ligne. Ce sont les 30ème et 31ème lignes qui portent l’erreur. iIl fallait, à mon modeste avis, dire :
Ainsi, pour une injection, un élément de F ne pourra jamais avoir plus d’un antécédent, le maximum d’antécédent est un.
Bonjour, en effet la phrase était mal formulée, je l’ai rectifié, merci pour votre remarque !
Super :)))
Bonjour,
Sauf erreur de ma part, pour que l’on dise qu’une « fonction » est injective, surjective ou bijective, il faut que cette fonction soit une application. En effet, une application est un cas particulier de la fonction où tout les éléments de l’ensemble de départ possède une unique image dans l’ensemble d’arrivée. Une fonction qui ne serait pas une application pourrai avoir un élément de l’ensemble de départ qui n’aurai aucune images (ex : f(x) = 1/x, en x=0, la fonction n’est pas définie). L’application, qui est donc la « restriction » d’une fonction à sont ensemble de départ, peut ensuite faire l’objet d’une injection, surjection ou bijection.
Pour infos, il y as : (soient E,F deux ensembles quelconques)
Les correspondances de E dans F (chaque éléments de E possèdent 0, 1 ou plusieurs images dans F, chaque éléments de F possèdent 0,1 ou plusieurs antécédents dans E).
Les fonctions de E dans F (chaque éléments de E possèdent 0, 1 images dans F, chaque éléments de F possèdent 0,1 ou plusieurs antécédents dans E).
Les applications de E dans F (chaque éléments de E possèdent une unique image dans F, chaque éléments de F possèdent 0,1 ou plusieurs antécédents dans E).
Les applications injectives de E dans F (chaque éléments de E possèdent une unique image dans F, chaque éléments de F possèdent 0,1 antécédent dans E).
Les applications injective de E dans F (chaque éléments de E possèdent une unique image dans F, chaque éléments de F possèdent 1 ou plusieurs antécédents dans E).
Les applications de E dans F (chaque éléments de E possèdent une unique image dans F, chaque éléments de F possèdent un unique antécédents dans E).
Bonjour,
Merci pour cette remarque judicieuse et pour votre commentaire, il est vrai que j’ai omis de dire que la fonction f devait être une application pour pouvoir dire que cette fonction est « injective, surjective ou bijective ». Je vais rajouter les définitions complètes pour éviter toute ambiguïté, comme par exemple :
Pour l’injection : « Soient E et F deux ensembles quelconques et f une application de E dans F. f est injective si et seulement si tout élément y de F possède au plus un antécédent par f. »
Toutefois, je pense que dans votre commentaire, vous vous avez oublié de dire pour l’avant dernier paragraphe que cela concernait les applications surjectives et que pour le dernier paragraphe cela concernait les applications bijectives. En tout cas, vos explications permettent d’améliorer encore davantage la compréhension de ces notions.
Cordialement,
Mon astuce n’est pas aussi complète car elle ne repose que sur la mémorisation des trois mots via une sorte de mot-valise « InSuBi » :)