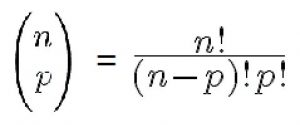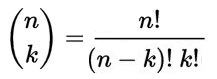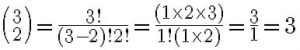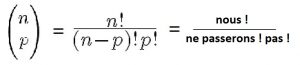Le Coefficient Binomial

Cet article vous propose de comprendre la formule du coefficient binomial, et de pouvoir la retenir grâce à une astuce mnémotechnique très particulière !

Le coefficient binomial est très utilisé en probabilité, et permet notamment de résoudre des problèmes sans faire d’arbre pondéré (qui peuvent atteindre des tailles très grandes). Le coefficient binomial est défini comme le nombre de chemins conduisant à k succès.

En langage mathématique, on dirait que le coefficients binomial $\textstyle{n \choose k}$ (que l’on prononce « k parmi n » ou « combinaison de k parmi n »), donne donc le nombre de parties de k éléments dans un ensemble total de n éléments, avec k ≤ n, (ce qui revient à dire que le coefficient binomial est le nombre de chemins conduisant à k succès).

La définition mathématique du coefficient binomial est la suivante :

(indigeste au premier coup d’œil..)

Le k du coefficient binomial $\textstyle{n \choose k}$ est une variable muette, c’est-à-dire qu’elle peut être remplacée par une autre lettre, comme c’est le cas ici où l’on remplace le k par un p.

Remarque :

La notation n! (n suivi d’un point d’exclamation, que l’on prononce « n factoriel ») correspond à la fonction factorielle ; avec n un entier naturel (un entier naturel est un nombre sans virgule et forcément positif, comme 0 ; 1 ; 2 …) ; la fonction factorielle est le produit des nombres entiers strictement positifs inférieurs ou égaux à n. Par exemple :

3! = 1×2×3 = 6
4! = 1×2×3×4 = 24
n! = 1×2×3×..×..×n

(Cas particulier pour 0 factoriel : 0! = 1)

Exemple d’application de cette formule :

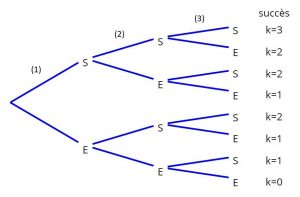
L’exemple suivant est une épreuve de Bernoulli, où l’on fait trois tirages ( n = 3 ), donc un arbre pondéré avec 3 étages. À chaque expérience, on note S un succès et E un échec. On s’intéresse uniquement au nombre de succès, qu’on note k (cela aurait aussi pu être la lettre p).

Dans l’exemple, on peut imaginer qu’on lance 3 fois une pièce d’or (n = 3 tirages), où le succès S correspond à l’événement «Pile» et l’échec E correspond à l’événement «Face», voici l’arbre de la situation :

On remarque qu’il existe 4 succès possibles (donc 4 valeurs différentes pour k) :

Pour k = 0 : il y a 1 chemin qui mène à 0 succès (soit aucune pièce donnant pile), on note
Pour k = 1 : il y a 3 chemins qui mènent à 1 succès, on note
Pour k = 2 : il y a 3 chemins qui mènent à 2 succès, on note
Pour k = 3 : il y a 1 chemin qui mène à 3 succès (soit toutes les pièces donnant pile), on note

Pour aller plus vite, on a l’habitude de remplacer l’arbre par la formule du coefficient binomial :

En remplaçant le n par 3, et k par 0, on obtient :

En remplaçant le n par 3, et k par 1, on obtient :

En remplaçant le n par 3, et k par 2, on obtient :

En remplaçant le n par 3, et k par 3, on obtient :

Bien sûr, cet exemple peut se faire rapidement avec l’arbre pondéré, mais lorsque cela se complique, il est intéressant de passer directement à la formule du coefficient binomial ! Maintenant, passons à l’astuce !

Astuce :

L’astuce pour retenir la formule du coefficient binomial $\textstyle{n \choose k}$ est assez spéciale et particulière… il faut avoir vu cette scène culte des seigneurs des anneaux : ICI

En effet, Gandalf dit à voix haute :

« Vous !
Ne passerez ! Pas ! »

Et bien pour nous, qui tentons de retenir la formule du coefficient binomial, il faut remplacer le ‘vous’ par ‘nous’, et se dire :

« nous !
ne passerons ! pas ! »

Pour :