La trigonométrie, c’est l’une des bases fondamentales qu’il faut maîtriser en maths, elle est partout ! Cependant, les formules de trigo ne sont pas si faciles à mémoriser (certes on peut les retrouver grâce à des démonstrations mathématiques, mais cela peut faire perdre du temps, il faut donc les connaître par cœur ! Ainsi, je vous propose quelques astuces mnémotechniques pour la trigonométrie !
Je vous conseille de vous reporter à chaque fois à l’image ci-dessous, car elle regroupe pratiquement toutes les astuces et formules de trigo !
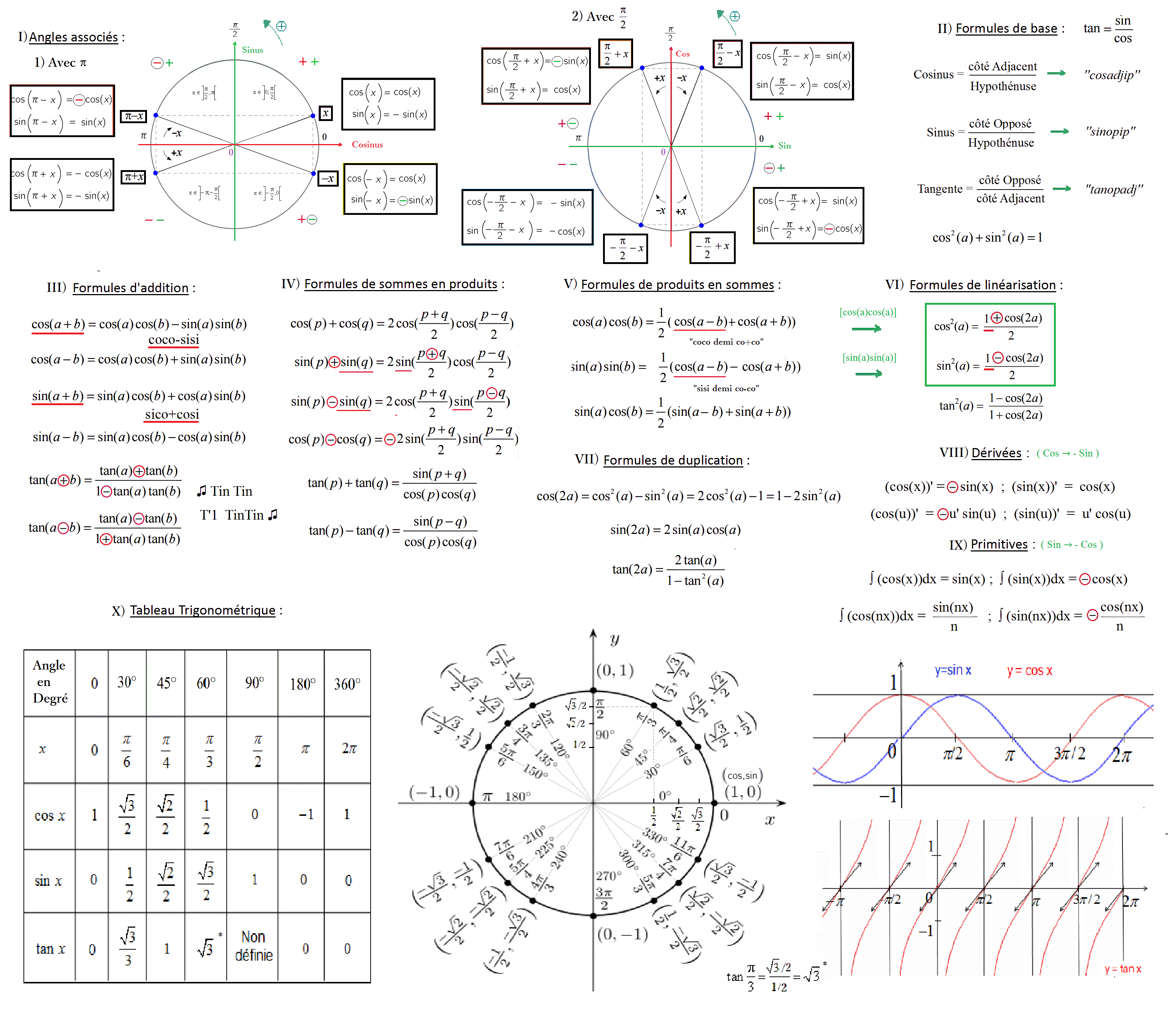
I) Angles associés :
1) Pour déterminer les angles associés à π, il faut toujours avoir le cercle trigonométrique en tête (en le reproduisant plusieurs fois, il est vite mémorisé), ensuite il faut considérer que l’axe des abscisses correspond au cosinus et que l’axe des ordonnées correspond au sinus. (En regardant l’image ci-dessus, on comprend mieux). Il faut toujours faire attention au sens donné (qui se trouve en haut du cercle avec un signe (+)), lorsqu’on commence à partir de π, pour déterminer cos(π-x), on lui retire x, ensuite il faut regarder où est-ce que l’on se situe, en l’occurrence sur cet exemple, on se trouve dans l’intervalle ]π/2 ; π[, ce qui correspond à un cosinus négatif et à un sinus positif (voir dessin les signes en vert pour sinus et en rouge pour cosinus), donc on obtient bien : cos(π – x) = – cos(x), ainsi que sin(π-x) = + sin(x).
2) Il en est de même pour déterminer les angles associés à π/2, mais cette fois-ci, il faut considérer que l’axe des abscisses correspond au sinus et que l’axe des ordonnées correspond au cosinus. En prenant l’exemple de cos(π/2 + x), on commence de π/2, puis on rajoute x, on regarde alors dans quel intervalle on se situe (ici ]π/2 ; π[ , et l’on remarque le sinus est négatif et que le cosinus est positif, on a donc cos(π/2 + x) = – sin(x), ainsi que sin(π/2 + x) = cos(x).
II) Formules de base :
Pour retenir que cosinus est égal au côté Adjacent sur l’Hypoténuse, il suffit de retenir « cosadjip » et de le dire le plus rapidement possible.
De même, pour sinus qui est égal au côté opposé sur l’Hypoténuse, on a : « sinopip »
Enfin, pour tangente qui est égal au côté opposé sur le côté Adjacent, on a : « tanopadj »
III) Formules d’addition :
1) cos(a+b) = cos(a)cos(b) – sin(a)sin(b) devient « coco-sisi » (ici le tiret les reliant correspond au (–) devant sin(a)sin(b)), pour mémoriser que c’est un (-), il faut penser que coco et sisi sont reliés, cela permet de ne pas confondre avec sin(a+b). Et pour obtenir cos(a-b), il suffit d’inverser ce fameux (-).
2) sin(a+b) = sin(a)cos(b) + cos(a)sin(b) devient « sico+cosi » (ici on peut voir qu’il y a un signe (+) devant cos(a)sin(b), pour le retenir que c’est un (+), il faut penser que le (+) symbolise la symétrie entre sin()cos() et cos()sin(), cela permet de ne pas confondre avec cos(a+b). Et pour obtenir sin(a-b), il suffit d’inverser ce fameux (+).
3) tan(a+b) = (tan(a)+tan(b))/(1 – tan(a)tan(b)) devient (en musique) ♫ Tin Tin T’1 TinTin ! ♫
Concernant les signes (c’est mieux de visualiser le dessin) le signe (+) de tan(a+b) se retrouve au numérateur, tandis qu’un signe (-) apparaît au dénominateur.
De même pour tan(a-b)= (tan(a)-tan(b))/(1+ tan(a)tan(b)), le signe (-) de tan(a-b) se retrouve au numérateur, tandis qu’un signe (+) apparaît au dénominateur.
IV) Formules de sommes en produits :(voir image ci-dessus pour comprendre les explications)
1) sin(p) + sin(q) = 2sin((p+q))/2)cos((p-q))/2), on peut remarque que le signe (+) devant le sin(q) se retrouve derrière le seul sin, derrière sin((p+q)/2).
sin(p) – sin(q) = 2cos((p+q))/2)sin((p-q))/2), on peut remarquer que le signe (-) devant le sin(q) se retrouve derrière le seul sin, derrière sin((p-q))/2).
Enfin, j’ai mis cos(p) – cos(q) = -2sin((p + q)/2)sin((p – q)/2) en dernier dans le classement, pour se souvenir que c’est le seul à posséder un signe (-) devant, on peut alors se dire que cos(p) + cos(q) est toujours positif (p et q de cos sont toujours contents quand ils sont additionnés ! A l’inverse, il sont malheureux, négatifs, quand ils sont soustraits…).
V) Formules de produits en sommes : (Cette partie est plus visuelle, c’est mieux avec l’image)
Pour retenir cos(a)cos(b) = (½)[cos(a-b)+cos(a+b)], on peut retenir « coco demi co+co »
Et pour sin(a)sin(b) = (½)[cos(a-b)+cos(a+b)] : « sisi demi co-co »
Par ailleurs, le VI) permet de se souvenir des signes du V)
En effet, on a cos²(a) = [1+(cos(2a)]/2 = cos(a)cos(a) = (½)[cos(a-a)+cos(a+a)] (« coco demi co+co »)
De même, on a sin²(a) = [1-(cos(2a)]/2 = cos(a)cos(a) = (½)[cos(a-a)-cos(a+a)] (« coco demi co-co »)
VIII) Dérivées : Lorsque cosinus dérive (sur l’eau), il se cogne, perd sa tête (son « co ») et se transforme en sinus négatif !
(cosinus)’ = – sinus & (sinus)’ = cosinus
(cos(x))’ = – sin(x) & (sin(x))’ = cos(x)
IX) Primitives : Lorsque sinus est intégré, il retrouve sa tête (son « co ») et se (re)transforme en cosinus négatif !
∫(sinus) = – cosinus & ∫(cosinus) = sinus
∫(sin(x))dx = – cos(x) & ∫(cos(x))dx = sin(x)
X) Tableau Trigonométrique : Le meilleur moyen de retenir les valeurs de ce tableau, c’est de connaître les courbes sinus et cosinus, ainsi que son cercle trigonométrique (voir image ci-dessus) ! Retenez toujours que la fonction cosinus admet son maximum 1 lorsqu’elle est à 0 (c’est-à-dire cos(0)=1), et que la fonction sinus passe par zéro en étant croissante (on peut se dire que cette courbe sinusoïdale est une vague qui mesure 1m hors de l’eau, puis 1m lorsqu’elle s’écrase au fond de l’eau, ainsi on obtient notre intervalle [-1; 1], et puisque le 0 correspond au milieu, ici, la surface de l’eau, on a sin(0)=0 & sin(π)=0.
Enfin, pour déterminer les valeurs dans le tableau pour tangente, il suffit d’utiliser la formule la plus importante : tan = sin/cos !
Autre astuce :
Si vous connaissez par coeur vos dérivées et primitives de cosinus et sinus, nous vous proposons de les utiliser pour vous souvenir à jamais des fameux cos(π/2 + x) et sin(x – π/2) !
En effet, nous avons vu plus haut, que les dérivées donnaient :
(cos(x))’ = – sin(x) & (sin(x))’ = cos(x)
Et bien, c’est la même pour (π/2 + x) :
cos(π/2 + x) = – sin(x) & sin(π/2 + x) = cos(x)
Ensuite, nous avons aussi vu que les primitives donnaient :
(sin(x))dx = – cos(x) & ∫(cos(x))dx = sin(x)
Et bien, c’est la même pour (x – π/2) :
sin(x – π/2) = – cos(x) & cos(x – π/2) = sin(x)
Ainsi, pour les retenir et ne pas les confondre, il faut se dire que dans le mot dérivée on a le terme « de » en premier, à la fois pour le 2 de pi/2 (pi sur 2), et le « de » du terme « de plus (de +) », on a donc dérivée : (π/2 + x) !
Ensuite, dans le mot primitive, on a le « m » de « moins (-) », et en se disant que la primitive est à la suite de la dérivée (pi/2 + x – pi/2 ), on a donc primitive : (x – π/2) !
Ainsi, le fait de connaître ses dérivées permet aussi de connaître l’influence de (π/2 + x) ; et connaître ses primitives permet aussi de connaître l’influence de (x – π/2) !
Remarque :
Les valeurs « cos (π) = -1 » et « cos (π/2) = 0 » sont souvent utilisées en physique et en maths, elles se retrouvent à l’aide de la courbe du cosinus, mais en cas de problème de visualisation de cette courbe, voici une astuce :
L’expression cos (π) fait penser au terme « copie », ainsi si l’on copie sur son voisin, on a -1 sur sa note, pour cos (π) = -1.
Et pour se souvenir que cos(π/2) = 0, on peut se dire que si l’on copie sur 2 voisins, cette fois-ci on a 0 au contrôle !
- Différence entre poulpe, pieuvre et calamar - 1 novembre 2021
- Différence entre Mitose et Méiose - 1 novembre 2021
- Les races de vache : les reconnaître - 17 septembre 2019
Je commence àl’utuliser sa m’intèresse