Les équations de Maxwell sont des lois fondamentales de la physique, et sont au nombre de quatre (Maxwell-Gauss, Maxwell-Faraday, Maxwell-Flux et Maxwell-Ampère). L’ensemble de ces équations se rapportent à l’électromagnétisme, et plus particulièrement à la description des phénomènes magnétiques, électriques, et lumineux.
- La formule de Maxwell-Gauss stipule que la divergence du champ électrique est proportionnelle à la distribution de charges électriques.
Avec le vecteur E qui est le champ électrique en V/m, q la distribution de charges en C/m³ et la permittivité diélectrique du vide εo en C/V/m.
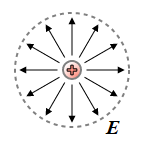
Cette équation signifie que le champ électrique (E) est divergeant (ou convergent en fonction du signe de la charge) à partir d’une source (qui est la charge (+) sur le schéma). Ainsi, div(E) est proportionnel à la distribution (ρ) des charges.
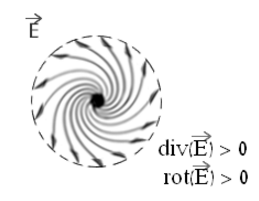
Remarque : Le rotationnel du champ électrique sur ce premier schéma est nul, contrairement au schéma qui va suivre avec l’équation de Maxwell-Faraday.
- La formule de Maxwell-Faraday correspond au phénomène d’induction et stipule que le rotationnel du champ électrique (E) est inversement (signe moins) proportionnel à la variation du champ magnétique au cours du temps (dB/dt).
Cette équation signifie que c’est la variation du champ magnétique (dB/dt) qui produit un champ électrique (E), et non le champ magnétique tout seul (B), (par exemple, une dynamo immobile sur un vélo n’alimente pas les lumières ; en revanche lorsque l’on roule, les lampes s’allument, car il y a variation du champ magnétique).
- La formule de Maxwell-Flux (aussi connue sous le nom de Maxwell-Thomson ou Maxwell-Kelvin ; Thomson et Kelvin étant une et même personne) stipule que la divergence du champ magnétique est nulle.
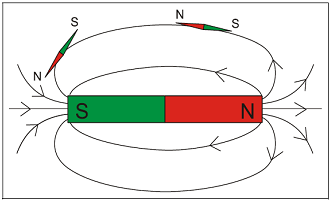
En effet, les lignes de champ magnétique ne divergent pas ; elles sortent d’un pôle (positif ou négatif) pour aller dans l’autre. Cela signifie aussi qu’il n’existe pas de monopôle magnétique (nord ou sud), en effet, tous les aimants possèdent deux pôles.
Remarque : L’aimant représente le pole nord et sud magnétique, tandis que les petites aiguilles de boussoles sur les lignes de champs indiquent le pole nord et sud géographique.
- La formule de Maxwell-Ampère stipule que le rotationnel du champ magnétique dépend d’une variation du champ électrique au cours du temps (dE/dt) et dépend également d’un courant électrique (μ0×j).
Avec le vecteur B qui est le champ magnétique en T (Tesla), la constante μ0 qui est la perméabilité magnétique du vide en T/A.m , le vecteur j qui est le vecteur densité de courant, c qui est une constante , la célérité (vitesse) de la lumière (reliée aux autres constantes par l’équation d’Alembert (εo×μ0×c² = 1)), et dE/dt la variation du champ électrique au cours du temps.
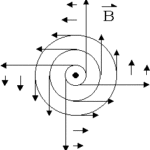
Remarque : sur le schéma ci-dessus, le fil où circule un courant est représenté par le point noir qui se trouve au milieu du cercle.
Astuces :
Après ces quelques descriptions des quatre équations de Maxwell, il est désormais question de les mémoriser sur le long terme !
Tout d’abord, il faut remarque que Maxwell-Faraday et Maxwell-Ampère sont les seules des quatre équations à posséder la lettre « r » dans leurs noms, donc ces deux équations font intervenir l’opérateur rotationnel !
Mais.. laquelle de ces deux équations applique un rotationnel sur le champ électrique (E) et sur le champ magnétique (B) ?!
Pour s’en souvenir, il suffit de s’intéresser aux premières lettres de Faraday et d’Ampère, en effet, il se trouve que la lettre F de Faraday est la lettre à côté du E dans l’alphabet, ainsi l’équation de Maxwell-Faraday fait intervenir rot(E) (les deux avec des vecteurs) !
De même, la première lettre A d’Ampère est juste à côté du B dans l’alphabet, ainsi l’équation de Maxwell-Ampère fait intervenir rot(B) (B avec un vecteur) !
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
- L’alphabet Arabe : les 28 lettres - 18 mars 2025
- Quelle est la différence entre Jaguar, Léopard et Guépard ? - 18 mars 2025

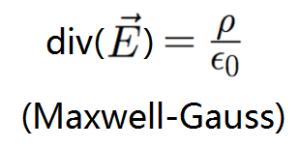
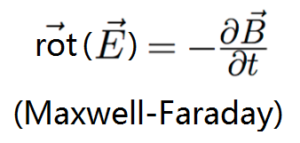
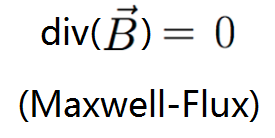
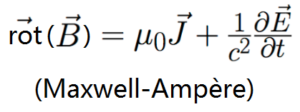
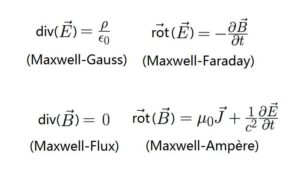

bonsoir
maintenant que faire de toutes ces notions abstraites?en tirer des consequences pratiques,par exemple construction d’un moteur ou d’un alternateur.moyensmateriels etude tres PRECISE de la fabrication.realisation.
pour la radio ,il existe d’autres chemins
Bien !
2 remarques :
– Sur les anciennes bicyclettes, ce qui s’appelait communément dynamo était en fait un alternateur. La nuance est importante.
– Le dernier paragraphe avec ces pseudo moyens de mémorisation ne sont pas à la hauteur du reste de l’article,
Pour Faraday, c’est simple: il a prêté son nom à l’unité de capacité Electrique, le Farad.
Pour Ampère … si c’est pas l’un c’est l’autre. Pas E, donc B, le champ magnétique
Ping : Electricité générale | Pearltrees
j’ai rien compris
c’est génial merci beaucoup
très bien explication, les schémas et les astuces c’est vraiment la génie
Merci beaucoup