Avez-vous déjà été confronté à un problème faisant intervenir des projections vectorielles ? Si oui, vous avez sûrement remarqué qu’il n’est pas toujours facile de faire des projections, et que celles-ci semblent la plupart du temps hasardeuses !
Et quand on lance une recherche sur internet pour comprendre les projections, on tombe toujours sur des cas particuliers, qui ne correspondent pas forcement à notre problème..
Cet article est donc là pour vous proposer une seule astuce, qui vous permettra de réussir pratiquement n’importe quelles projections vectorielles !
Pour réaliser cette astuce, nous allons procéder en trois étapes ; une fois qu’elles seront maîtrisées, vous serez capable de faire votre projection en quelques secondes !
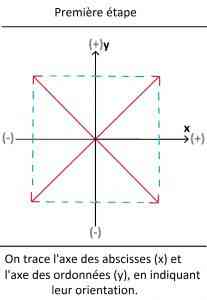
Première étape :
La première étape consiste à prendre un bout de papier, puis à tracer l’axe horizontal (celui des abscisses x), et l’axe vertical (celui des ordonnées y), en les orientant ; ensuite il faut tracer quatre flèches en diagonale (celles qui sont représentées en rouge).
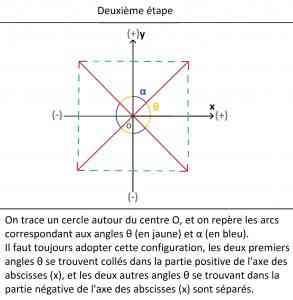
Deuxième étape :
La deuxième étape consiste à tracer un cercle autour du centre O, et on repère ensuite les arcs correspondant aux angles θ (en jaune) et aux angles α (en bleu). Il faut toujours adopter cette configuration, les deux premiers angles θ se trouvant dans la partie positive de l’axe des abscisses (x) sont collés, tandis que les deux autres angles θ se trouvant dans la partie négative de l’axe des abscisses (x) sont séparés. C’est l’inverse pour les angles α.
Troisième étape :
La troisième étape consiste à renommer les axes des abscisses et des ordonnées par des cosinus et des sinus.
L’astuce (si le cas se présente) consiste à reproduire l’un des deux schémas (ci-dessous) sur un bout de papier, puis le comparer avec la situation de l’exercice (c’est-à-dire, regarder quelle est l’orientation de la flèche rouge par rapport à l’axe des abscisses et des ordonnées). Pour mieux visualiser, trois exemples vous seront proposés juste après les explications de ces deux schémas.
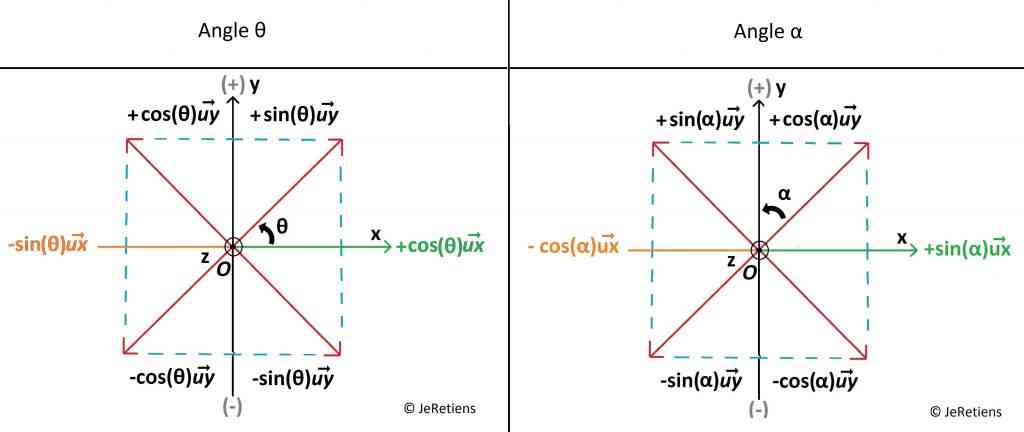
Cas où l’angle correspond à θ :
Pour l’axe horizontal (x) :
L’axe des abscisses (x) est divisé en deux parties,
La partie colorée en orange, à gauche, correspond à la partie négative de l’axe x, elle correspond à – sin(θ)
La partie colorée en vert, à droite, correspond à la partie positive de l’axe x, elle correspond à + cos(θ)
Pour l’axe vertical (y) :
L’axe vertical (y) divise l’axe (x) en deux parties, nous venons de le voir juste au-dessus, ainsi on a une expression différente de chaque côté :
Les ± sin(θ) se placent à droite, ils doivent être différents du cos(θ)
qui se trouve lui aussi à droite, mais pour l’axe (x).
Les ± cos(θ) se placent à gauche, ils doivent être différents du – sin(θ)
qui se trouve lui aussi à gauche, mais pour l’axe (x).
En soit, pour se souvenir de ce schéma, il suffit de placer en premier le cos(θ) sur la partie positive de l’axe (x), puis les ± sin(θ)
de chaque côté de la partie positive de l’axe (x), puis de faire l’inverse pour la partie négative de l’axe de (x).
Cas où l’angle correspond à α : (c’est le cas inverse de l’ange θ)
Pour l’axe horizontal (x) :
L’axe des abscisses (x) est divisé en deux parties,
La partie colorée en orange, à gauche, correspond à la partie négative de l’axe x, elle correspond à – cos(α)
La partie colorée en vert, à droite, correspond à la partie positive de l’axe x, elle correspond à + sin(α)
Pour l’axe vertical (y) :
L’axe vertical (y) divise l’axe (x) en deux parties, nous venons de le voir juste au-dessus, ainsi on a une expression différente de chaque côté :
Les ± cos(α) se placent à droite, ils doivent être différents du sin(α)
qui se trouve lui aussi à droite, mais pour l’axe (x).
Les ± sin(α) se placent à gauche, ils doivent être différents du – cos(α)
qui se trouve lui aussi à gauche, mais pour l’axe (x).
Nous allons maintenant passer à la mise en pratique de cette astuce !
Exemples d’application :
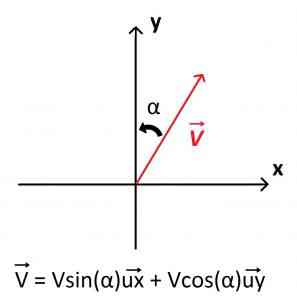
1) En comparant la situation ci-dessous aux deux schémas de l’astuce, on reconnaît le cas où l’angle correspond à α, on obtient donc : = V×sin(α)
+ V×cos(α)
(Vous avez sans doute remarqué le V devant sinus et cosinus, ce V correspond à la norme du vecteur
, il faut systématiquement le mettre devant le cos et le sin, car la norme est comprise dans la formule).
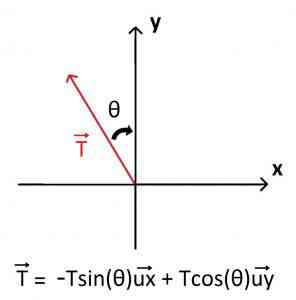
2) En comparant la situation ci-dessous aux deux schémas de l’astuce, on reconnaît le cas où l’angle correspond à θ, on obtient donc : = -T×sin(θ)
+ T×cos(θ)
3) Ce dernier exercice est une application des projections vectorielles concernant les forces, en particulier par rapport au Poids :
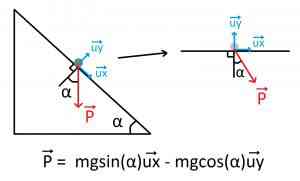
En comparant la situation ci-dessous aux deux schémas de l’astuce, on reconnaît le cas où l’angle correspond à α, on obtient donc (en retournant le schéma) : = mg×sin(α)
– mg×cos(α)
(le poids est la force de la pesanteur, la norme du poids est donc égale à m×g (m pour la masse en kg, et g pour l’accélération de la pesanteur en m·s-2, ce qui par ailleurs est bien homogène à une force N : kg.m·s-2)).
Cette astuce sur les projections permet d’être rapide, mais aussi d’éviter des calculs faisant intervenir des sin(π/2 + α), cos(α – π/2), etc.. dans lesquels on peut facilement se tromper ! Cependant, l’astuce qui vous a été présentée ne fonctionne que dans les cas décrits plus haut, avec les angles θ et α, mais dans la majorité des cas, les projections ont lieu sur ces angles !
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
- L’alphabet Arabe : les 28 lettres - 18 mars 2025
- Quelle est la différence entre Jaguar, Léopard et Guépard ? - 18 mars 2025


Maiiiis, c’est du génie !! Mercie beaucoup
bonjour,
je préfère la méthode classique de projections , pour le plan incliné ,quand x est parallèle à la plus grande pente et y sa perpendiculaire ou l’autre quand x est parallèle au sol et y perpendiculaire ,on se retrouve dans les signes négatifs ou positifs aisément ,il suffit d’y travailler
cordialement
robert vives