La constante des aires

En physique, dans le domaine de la mécanique, la constante des aires est assez utile pour certains calculs liés aux forces centrales (force dirigée vers
un point fixe), telles que la force gravitationnelle (de Newton) ou la force électrostatique (de Coulomb).

Lorsque le moment cinétique (ou « moment angulaire », qui est une grandeur vectorielle utilisée pour décrire la rotation d’un système) d’une force centrale est conservée, il existe deux conséquences : un mouvement plan et la loi des aires (2ème Loi de Kepler).

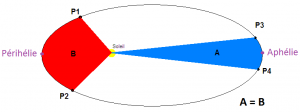
Cette loi des aires stipule que la vitesse aréolaire A’ (vitesse de balayage d’une aire par un rayon) est constante pour un mouvement à force centrale, ainsi le vecteur position r (qui correspond au rayon) balaie des surfaces égales en des intervalles de temps égaux (comme sur l’illustration ci-dessous).

Après la combinaison de plusieurs expressions (que nous n’allons pas expliciter ici, car seule la mémorisation de la formule nous intéresse ici), on obtient la constante des aires, qui relie :

C = θ’ × r² = r × v = L/m

Avec C la constante des aires (en m²/s), θ (thêta) est l’angle parcouru (en rad), θ’ (thêta point) est la vitesse angulaire (en rad/s), v est la vitesse linéaire (en m/s) , r correspond au rayon qui balaie l’aire (en m), L correspond au moment cinétique (soit en kg.m²/s, en effet le moment cinétique correspond au produit vectoriel de la distance (en m) ʌ et de la quantité de mouvement (en kg.m/s)) et m correspond à la masse (en kg).

On remarque bien que ces trois relations sont homogènes à des m²/s , l’unité de la constante des aires !

Cette constante des aires permet de dire que l’aire aréolaire A’ (dérivée de l’aire par rapport au temps) est constante, en effet A’ = C/2 (de façon simplifiée).

Astuce :

Pour se souvenir de ces différentes relations liées à la constante des aires, il faut se dire la phrase suivante : « Courrrs vite loin de moi ! »

« Cθurrrs vite Loin de moi ! » pour C = θ’r² = rv = L/m

En effet, le c de courrrs correspond au c de la constante des aires, le θ de cθurrrs correspond à l’angle (thêta point), les deux premiers r de courrrs correspondent au r², ensuite le troisième r correspond à rv, le r qui est multiplié par le v (qui correspond au v de vite, enfin le L correspond au L de Loin et le m de moi correspond au m du moment cinétique.

Une autre astuce, qui prend moins de termes en compte, consiste à dire « C’est Hervé ! » pour C = rv, permettant de se souvenir de l’unité de la constante des aires en m²/s.