Les trois lois de Kepler sont fondamentales en astronomie, et décrivent les propriétés principales du mouvement des planètes autour du Soleil.
Ces trois lois ont été découvertes en 1604 et 1618 par Johannas KEPLER (astronome et physicien allemand), à partir des observations et mesures de la position des planètes faites par Tycho Brahe (danois).
Cet article vous propose de découvrir ces trois lois, et de retenir la troisième par cœur grâce à une astuce mnémotechnique en fin d’article !
La première loi de Kepler (Loi des orbites) : Les planètes décrivent des trajectoires elliptiques autour de l’un des foyers, celui-ci étant occupé par le Soleil.

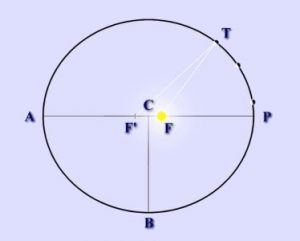
Remarque : Dans le référentiel héliocentrique (aussi appelé référentiel de Kepler), le Soleil occupe toujours l’un des deux foyers de la trajectoire elliptique des planètes qui gravitent autour de lui.
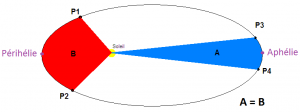
La deuxième loi de Kepler (Loi des aires) : Le rayon vecteur (Soleil-Planète) balaie des aires égales pendant des durées égales. Comme on peut le constater sur l’illustration ci-dessous, les aires A et B sont égales.
Remarque : La vitesse d’une planète devient plus grande lorsque la planète se rapproche du Soleil. Cette vitesse est maximale au voisinage du rayon le plus court (périhélie), et minimale au voisinage du rayon le plus grand (aphélie), (astuce pour retenir la différence entre apocentre et péricentre : ici)
La troisième loi de Kepler (Loi des périodes) : Cette troisième loi de Kepler stipule que le carré de la période de révolution (T²) est proportionnel au cube de la distance au Soleil (a³). Ainsi, le mouvement des planètes du système solaire vérifie l’équation suivante :
Avec T la période de révolution de la planète autour du Soleil, et a le demi grand axe de l’ellipse.
Remarque :
Dans le cas général où la trajectoire est elliptique, l’équation s’écrit :
T²/a³ = (4pi²)/GM = constante
Avec T la période de révolution de la planète autour du Soleil, a le demi grand axe de l’ellipse, G la constante gravitationnelle, M la masse de l’étoile, et m la masse de l’objet en orbite (normalement on devrait avoir G(M+m), mais puisque la masse m est négligeable devant masse M, m n’entre pas en compte dans la formule).
Astuce pour la 3e loi de Kepler :
En cas d’oublie de la formule, je vous propose de retenir et d’utiliser cette phrase, avec laquelle on peut retrouver tous les termes de l’équation :
Kepler, si t’as pas faim, « T’as qu’à pas manger » !
Retenez juste : « T‘as qu’à pas manger » !
Le T‘ correspond à la période de révolution de la planète autour de l’étoile (T), le as correspond au demi grand axe de la trajectoire elliptique (a), le qu’à au 4, le p de ‘pas‘ à la lettre pi (π), le a de ‘pas’ correspond au ‘a‘ de ‘carré’ (²), et enfin, le mot ‘manger‘ correspond d’abord à la masse de l’étoile (M), puis à la constante de la gravitation universelle (G).
En ce qui concerne le carré sur le T² et le cube sur le a³ , il faut compter dans le sens croissant vers le bas, et se dire que le ² est avant le ³ !
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
- L’alphabet Arabe : les 28 lettres - 18 mars 2025
- Quelle est la différence entre Jaguar, Léopard et Guépard ? - 18 mars 2025

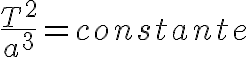
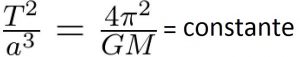
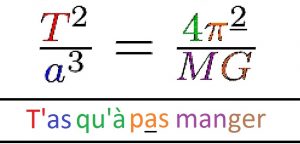
Ping : FJ Mathématiques Lycée (jadotf) | Pearltrees
Euréka ! (403 tours de manège après les découvertes de Kepler)
L’Assemblée Nationale et le Sénat viennent d’échouer à se mettre d’accord sur les termes de la modification de la Constitution d’un petit bout de planète, pour une histoire de conséquences incertaines si on se mettait à privilégier, en France, la lutte contre le dérèglement climatique, sur la planète Terre, par rapport à d’autres trucs que je ne me rappelle pas.
Bon alors, c’est simple, Yaka décider qu’une année fait plus que 365 jours ! comme çà « T » va augmenter et comme « T » au carré divisé par « a » au cube est une constante ( si on récupère Monsieur Bronson ), alors « a » va augmenter aussi. Du coup, si on est plus loin du Soleil, alors on recevra moins d’énergie et le réchauffement climatique va s’atténuer.
La cerise sur le gâteau, c’est qu’on va vieillir moins vite.
Atmosphériquementr vôtre,
Excellent explication
Merci.