La formule de Varignon est utile pour l’étude de systèmes mécaniques, comme l’étude de poulies, de roues de brouette, vélo ou encore de voiture.
La formule de Varignon est donnée par la relation suivante :
Avec G le centre de la roue (ou sphère selon l’exercice), I le point d’intersection entre la roue et le sol (ici on a une pente, mais le sol peut aussi être horizontal), V(G) la vitesse en G, V(I) la vitesse en I, et ω le vecteur rotation.
Remarque :
– L’ordre du produit vectoriel ω^IG est important, car a^b et b^a sont des vecteurs opposés où b^a = – (a^b).
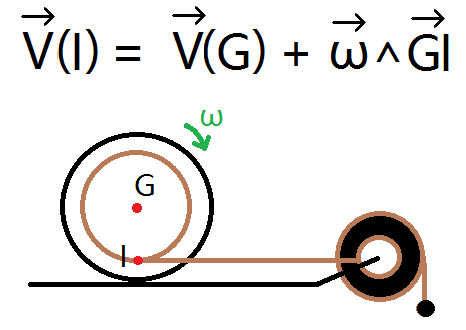
– Lorsque le point I appartient au sol et qu’il n’y a pas de glissement, V(I) = 0, mais si le point I n’appartient pas au sol, c’est-à-dire qu’il n’est pas placé entre la roue et le sol, mais, par exemple, entre la roue et un fil (comme c’est le cas avec une poulie), alors V(I) n’est plus égal à 0. Dans ce cas, la formule de Varignon peut aussi s’écrire sous la forme :
Astuce :
L’astuce consiste à penser au mot Glissement, qui comporte en premier un G puis un I, ainsi la formule commence par un V(G) puis est égal à un V(I), et ensuite, il y a une antisymétrique à la fin de la formule avec le vecteur IG.
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
- L’alphabet Arabe : les 28 lettres - 18 mars 2025
- Quelle est la différence entre Jaguar, Léopard et Guépard ? - 18 mars 2025

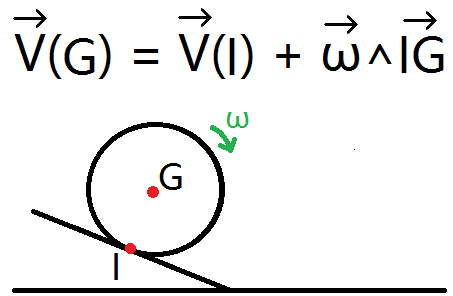
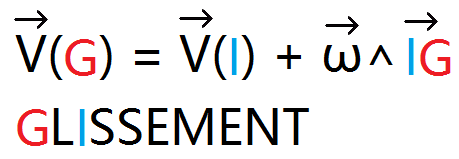


Je connaissais pas! Plutôt bien expliqué et facile à mémoriser. J’ai fait un tour sur tes astuces et articles scientifiques, tip top!