Ensembles de Nombres : Comprendre ℕ, ℤ, D, ℚ, ℝ en Maths

En mathématiques, nous travaillons avec 5 grands ensembles de base, qui permettent de manipuler les nombres. Ces ensembles sont parfois complémentaires et peuvent aussi se distinguer par les types de nombres qu’ils contiennent. Une étude, du plus petit au plus grand de ces 5 grands ensembles de base (il en existe d’autres), nous permet non seulement de définir et de présenter chaque ensemble, mais aussi de ressortir avec des exemples à l’appui sur leurs différences.
Ces ensembles sont: ℕ ℤ ℚ et ℝ.

Sommaire de l'article :

En Bref : Les 5 grands ensembles de nombres fondamentaux

ℕ (Naturels) : Nombres positifs ou nuls (0, 1, 2…).
ℤ (Relatifs) : Nombres entiers, positifs ou négatifs (…-1, 0, 1…).
D (Décimaux) : Nombres à virgule finie (ex: 2.5, -0.75).
ℚ (Rationnels) : Nombres exprimables sous forme de fraction a/b (ex: 1/3, 5/4).
ℝ (Réels) : Regroupe tous les rationnels et les irrationnels (ex: π, √2).
Relations d’inclusion : Chaque ensemble est inclus dans le suivant, formant une hiérarchie : ℕ ⊂ ℤ ⊂ &decimals; ⊂ ℚ ⊂ ℝ.
Moyen mnémotechnique : « NeZ Du CURé » pour mémoriser l’ordre des symboles (ℕ, ℤ, D, ℚ, ℝ).

L’ensemble ℕ

C’est l’ensemble des nombres entiers naturels. Un entier naturel est un nombre positif ou nul, permettant de compter des objets.

Exemples : 0, 1, 2, 3, 4, 5, 6, etc.

L’ensemble ℤ

C’est l’ensemble des nombres entiers relatifs. Un entier relatif est, non seulement, un entier naturel, mais se présente aussi comme un entier naturel muni d’un signe positif ou négatif.

Exemples : ….-5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, +7, +8, etc.

L’ensemble D

C’est l’ensemble des nombres décimaux relatifs. Un nombre décimal relatif est, non seulement, un nombre entier relatif, mais peut aussi être un nombre à virgule flottante, positif ou négatif.

Exemples : ….-5, -4, -4.2, -3, -2, -1.5, -1, 0, +0.7, +1, +2, +2.4, +3, +4, +5, +6, +6.75 +7, +8, etc.

L’ensemble ℚ

C’est l’ensemble des nombres rationnels. Un nombre rationnel est, non seulement, un nombre décimal relatif, mais peut aussi être un nombre qui peut s’exprimer avec le quotient de deux entiers relatifs. Le dénominateur étant non nul.

Exemples : ….-5/4, -4, -4.2, -3, -2, -1.5, -1/2, 0, +0.7, +1, +2, +2.4, +3, +4/5, +5, +6, +6.75, +7/2, +8

L’ensemble ℝ

C’est l’ensemble des nombres réels. Un nombre réel est non seulement un nombre rationnel, mais peut aussi être un nombre dont le développement décimal est infini, et non périodique.

Exemples : ….-5/4, -4, -4.2, -3, -2, -1.524, -1/2, 0, +0.7, +1, +2, +2.41, +3, +4/5, +5, +6, +6.75, +7/2, +8…

Comprenons

ℕ est inclus dans ℤ.
ℤ est inclus dans D.
D est inclus dans ℚ.
ℚ est inclus dans ℝ.

Exprimé mathématiquement cela donne:

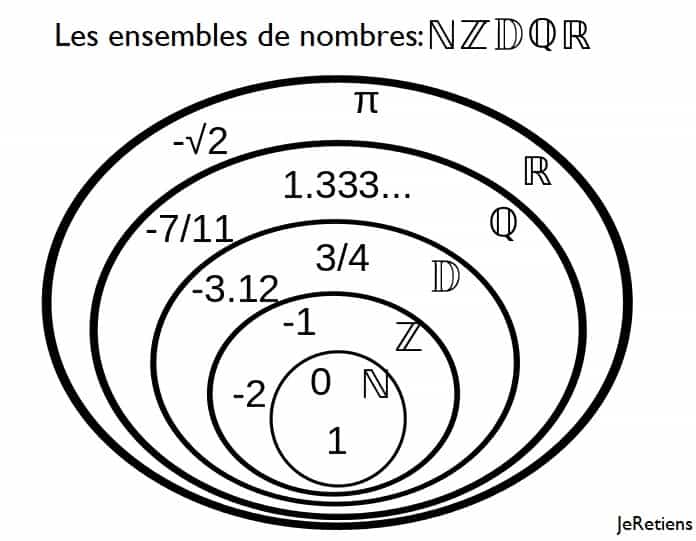
Ensemble des nombres entiers naturels, relatifs, décimaux, rationnels et réels — Relations d’inclusion entre les différents ensembles de nombres, des nombres naturels aux nombres réels.

Pour mémoriser les symboles des ensembles de nombres pensez à ce moyen mnémotechnique: « NeZ Du CURé. »

• ℕ : ensemble des entiers naturels
• ℤ : ensemble des entiers relatifs
• D : ensemble des nombres décimaux
• ℚ : ensemble des nombres rationnels
• ℝ : ensemble des nombres réels

Questions fréquentes sur les ensembles de nombres (FAQ)

Que représente l’ensemble ℕ (N) ?

L’ensemble ℕ représente les nombres entiers naturels, c’est-à-dire les nombres entiers positifs ou nuls : 0, 1, 2, 3, etc.

Que contient l’ensemble ℤ (Z) ?

ℤ est l’ensemble des entiers relatifs, c’est-à-dire tous les entiers positifs, négatifs et le zéro : -3, -2, -1, 0, 1, 2, 3, etc.

Que signifie l’ensemble D (D) ?

L’ensemble D regroupe les nombres décimaux, c’est-à-dire les nombres pouvant s’écrire sous forme d’une fraction avec un dénominateur 10, 100, 1000, etc. Exemple : 1,2 ; 0,005 ; -3,75.

Quelle est la définition de l’ensemble ℚ (Q) ?

ℚ représente les nombres rationnels, c’est-à-dire tous les nombres pouvant s’écrire sous la forme d’une fraction a/b, où a et b sont des entiers et b ≠ 0.

Que contient l’ensemble ℝ (R) ?

L’ensemble ℝ est l’ensemble des nombres réels : il regroupe tous les nombres rationnels (comme 1/2 ou -3) et les irrationnels (comme √2, π ou e).

Quels sont les symboles usuels des ensembles de nombres ?

Voici les principaux symboles : ℕ (nombres naturels), ℤ (entiers relatifs), D (décimaux), ℚ (rationnels), ℝ (réels). Ils sont utilisés pour classifier les nombres selon leurs propriétés.

Quelle est la distinction principale entre un nombre décimal (D) et un nombre rationnel (ℚ) ?

Un nombre décimal a un nombre fini de chiffres après la virgule (ou une partie décimale nulle), tandis qu’un nombre rationnel peut avoir un développement décimal infini mais périodique (comme 1/3 = 0,333…). Tous les décimaux sont rationnels, mais tous les rationnels ne sont pas décimaux.

Qu’est-ce qu’un nombre irrationnel et à quel ensemble appartient-il ?

Un nombre irrationnel est un nombre réel dont le développement décimal est infini et non périodique. Il ne peut pas s’exprimer comme le quotient de deux entiers. Des exemples célèbres sont la constante pi (π) ou la racine carrée de 2 (√2). Les nombres irrationnels appartiennent à l’ensemble ℝ (Réels).

Pourquoi ces ensembles de nombres sont-ils importants en mathématiques ?

Ces ensembles fournissent une structure fondamentale pour classer et comprendre les nombres. Ils sont essentiels pour définir des opérations, résoudre des équations, et poser les bases de domaines mathématiques plus avancés comme l’analyse, la topologie ou l’algèbre.

Comment la relation d’inclusion s’applique-t-elle entre les ensembles de nombres ?

La relation d’inclusion (⊂) signifie qu’un ensemble est contenu entièrement dans un autre. Pour les ensembles de nombres, cela signifie que tout nombre naturel est aussi un entier relatif, qui est aussi un décimal, qui est aussi un rationnel, et qui est enfin un réel (ℕ ⊂ ℤ ⊂ D ⊂ ℚ ⊂ ℝ).

Existe-t-il d’autres ensembles de nombres au-delà des réels ?

Oui, l’ensemble le plus vaste couramment utilisé est celui des nombres complexes (ℂ), qui inclut tous les nombres réels et permet de résoudre des équations qui n’ont pas de solution dans les réels (comme x² = -1). On parle aussi parfois de nombres entiers naturels non nuls (ℕ*).

Conclusion

En parcourant les cinq grands ensembles de nombres – les naturels (ℕ), les entiers relatifs (ℤ), les décimaux (D), les rationnels (ℚ) et les réels (ℝ) – nous avons découvert une hiérarchie fondamentale qui structure tout l’univers des mathématiques. Chaque ensemble, du plus simple au plus complexe, enrichit notre capacité à manipuler et à comprendre les quantités, en englobant le précédent et en introduisant de nouvelles propriétés. Maîtriser ces distinctions et leurs relations d’inclusion est une étape essentielle pour quiconque souhaite explorer les profondeurs des mathématiques, car ils forment la base sur laquelle reposent des concepts bien plus avancés. Ces ensembles ne sont pas de simples catégories, mais les piliers mêmes de la logique numérique.