Si avant de lire cet article vous ne vous souvenez plus de vos formules géométriques, voici 3 astuces qui vous permettront de ne plus jamais les oublier, notamment pour le cercle, le cylindre, et la sphère ! (Nous vous conseillons de vous reporter aux images à chaque fin d’astuce, pour une meilleure compréhension)
Si vous souhaitez avoir des bases complémentaires consultez notre article sur la différence entre le cercle et la sphère.
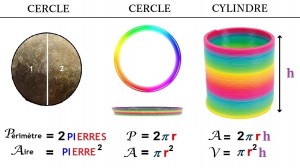
Le Cercle :
Le périmètre d’un cercle (2πR) et l’aire d’un cercle (πR²), possèdent les mêmes « composantes », il suffit de retenir une formule pour retrouver l’autre, et pour cela il faut se dire qu’on a besoin de deux pierres pour calculer la circonférence (synonyme de périmètre), oui, ‘deux’ ‘pi’ ‘erre’ pour 2piR (2π R) !
Ensuite, le ‘2’ présent dans les deux formules, est positionné différemment suivant la formule utilisée ; ainsi, lorsqu’on cherche à obtenir l’aire du cercle, on utilise (πR²) où le ‘2’ est une puissance, il faut toujours penser au fait qu’une aire est forcément au carré, contrairement au périmètre (qui n’est pas au carré).
Le Cylindre :
Pour retenir l’aire (latérale) d’un cylindre (2πRh), il faut imaginer un Slinky (c’est un jouet en forme de ressort, voir illustration en-dessous), lorsqu’on l’écrase, on ne voit qu’un cercle, donc le périmètre est le même qu’un cercle (2πR).
Ensuite, lorsque le Slinky revient à sa forme initiale, sa hauteur a augmenté, le jouet prend la forme d’un cylindre, le périmètre n’est alors plus le même. Désormais, pour obtenir l’aire latérale de ce cylindre, il faut multiplier le périmètre du cercle par ‘h’ la hauteur ! Finalement, on obtient l’aire (latérale) du cylindre : 2πRh.
Pour retenir le volume d’un cylindre ((πR²)*h), c’est le même principe, il faut multiplier l’aire du cercle par ‘h’ la hauteur, et on obtient ainsi le volume du cylindre : (πR²)*h.
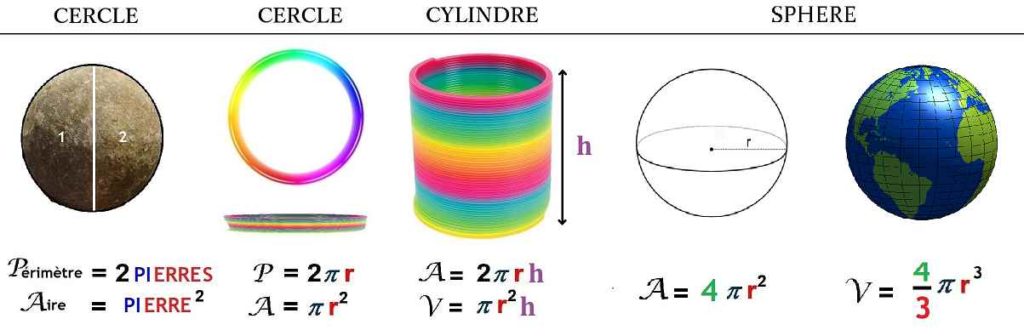
La Sphère :
Les formules de l’aire d’une sphère (4πR²) et du volume d’une sphère ((4/3)πR³) peuvent être mémorisées grâce à l’astuce suivante :
Pour le volume, (4/3)πR³) se prononce « quatre tiers pi R cube », on remarque alors une rime entre tiers et R, cela permet de ne pas confondre 3/4 (trois quart) et 4/3 (quatre tiers) dans la formule.
Pour l’aire, (4πR²), il faut imaginer ou dessiner une sphère avec à l’intérieur un cercle, en effet l’aire d’un cercle est de piR², qu’il faut ensuite multiplier par 4, et on retrouve le 4πR².
- Les trois singes de la sagesse : Mizaru, Kikazaru, Iwazaru - 18 décembre 2025
- Pâte brisée, sablée ou feuilletée ? - 11 décembre 2025
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
Rejoignez-nous sur Instagram !
Découvrez nos infographies et astuces : @JeRetiensNet

merci bien !
Thank you