Savez-vous en quoi s’exprime une force ? Si oui, sauriez-vous décomposer cette unité ? Si non, ce n’est pas grave du tout, car vous allez désormais le savoir, quelque soit vos connaissances en physique !
Tout d’abord, une FORCE s’exprime en Newton (N), c’est-à-dire en kg.m.s-2 : cette unité peut s’obtenir, de deux manières différentes.
La première est rigoureuse, tandis que la deuxième (plus originale) est moins scientifique.
Première Méthode (rigoureuse) : On utilise la deuxième loi de Newton (Principe Fondamental de la Dynamique, PFD), ainsi de façon simplifié on a : F = m.a avec normalement une flèche sur F et sur a car ce sont des vecteurs ; m est la masse en kg, a l’accélération en m.s-2 (l’accélération est la dérivée d’une vitesse qui s’exprime en m.s-1).
Ainsi on va faire une analyse dimensionnelle (c’est à dire que l’on va rassembler les unités, avec ici, la Masse [M] = kg (kilogramme), le Temps [T] = s (seconde), et la Longueur [L] = m (mètre)).
On a [F] = [m][a], or [F] = N, [m] = M, et [a] = LT-2, donc on obtient N = M.L.T-2 , donc N = kg.m.s-2, ainsi la somme des forces ( F) (dans un système) s’exprime en kg.m.s-2, soit en N.
Par ailleurs, à titre d’information :
On appelle un système, un ensemble d’éléments interagissant entre eux selon certains principes, par exemple une pomme (de masse m) tombant d’un pommier est un système, dans lequel des forces s’exercent sur la pomme en chute (notamment le poids qui entraîne la pomme (force motrice) ; les frottements avec l’air constituent aussi une force (résistante), mais cette force est si négligeable par rapport au poids, qu’elle n’entre pas toujours en compte lors de calculs).
Deuxième méthode (moins rigoureuse) : Pour retenir que N : kg.m.s-2 , voici une astuce très imagée, que l’on peut reproduire sur un bout de papier (voir illustration ci-dessous), mais pas très rigoureuse mathématiquement parlant. (Sur ce graphique-dessin, le choix des axes est arbitraire, ici on a choisi que l’axe des ordonnées (vertical) serait dirigé vers le bas (vers du positif), et l’axe des abscisses (horizontal) dirigé vers la droite (vers du positif)), les axes ne sont pas obligatoires, on peut simplement dessiner le N, puis rajouter les flèches (kg, m, s-2), mais ici les axes permettent de mieux comprendre le « s-2 » du N = kg.m.s-2.
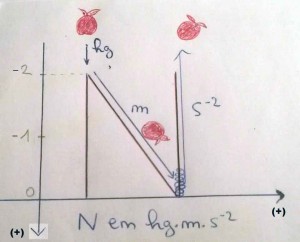
Cette astuce est toujours en rapport avec la fameuse pomme (de Newton) qui, d’après la légende, lui serait tombée sur la tête en 1666, et fut à l’origine de sa théorie sur la gravitation, qui explique l’attraction entre les corps (sa troisième loi).
Il faut imaginer qu’une pomme en métal de 1 kg tombe sur le premier sommet de la lettre N (c’est-à-dire le plus à gauche), puis imaginer qu’elle roule sur la diagonale du N de longueur 1 m, jusqu’à arriver en bas du N, là où il faut une nouvelle fois imaginer qu’il y ait un système de ressort qui projette la pomme dès qu’elle arrive en bas, ainsi elle est très vite envoyée dans les airs, soit en 1s^-2, en effet 1s^-2 car la pomme a dû remonter, dans le sens inverse de sa chute, 2 fois la position initiale de sa chute au premier sommet du N, (revoir illustration ci-dessus pour mieux comprendre).
- Différence entre poulpe, pieuvre et calamar - 1 novembre 2021
- Différence entre Mitose et Méiose - 1 novembre 2021
- Les races de vache : les reconnaître - 17 septembre 2019
