La trigonométrie est sans aucun doute l’une des pierres angulaires des mathématiques et de nombreuses sciences (physique, ingénierie, astronomie…). Que ce soit pour résoudre des problèmes de géométrie, analyser des ondes ou modéliser des phénomènes périodiques, ses formules sont omniprésentes. Cependant, leur mémorisation peut s’avérer un véritable casse-tête, même pour les plus assidus !

Sommaire de l'article :

Certes, on peut toujours les retrouver par des démonstrations ou en se basant sur le cercle trigonométrique, mais en situation d’examen ou quand le temps est compté, les connaître « par cœur » devient un atout indéniable. C’est pourquoi nous avons compilé pour toi les meilleures astuces mnémotechniques pour la trigonométrie, afin de te simplifier la vie et de te faire gagner un temps précieux.

Pour tirer le meilleur parti de cet article, nous te conseillons de te reporter régulièrement à l’image principale ci-dessous. Elle est un véritable condensé visuel de la plupart des astuces et des formules fondamentales de la trigonométrie.

En bref : Maîtriser la trigonométrie avec des astuces mnémotechniques

Angles associés : Visualise le cercle trigonométrique et les signes des sinus/cosinus en fonction des intervalles (pi-x, pi+x, etc.).
Formules de base (SOH CAH TOA) : Astuces « cosadjip », « sinopip », « tanopadj » pour les rapports dans le triangle rectangle.
Formules d’addition : « Coco-sisi » pour le cosinus et « sico+cosi » pour le sinus, avec une astuce musicale pour la tangente.
Transformations sommes-produits / produits-sommes : Règles des signes et associations visuelles.
Dérivées et Primitives : Des histoires pour retenir les transformations de cosinus et sinus.
Tableau trigonométrique : Comprendre les courbes et utiliser tan = sin/cos.

Les formules de trigonométrie, facile ! Toutes les astuces mnémotechniques

Q: Pourquoi apprendre les formules de trigonométrie par cœur ?

Bien qu'it soit possible de les retrouver par démonstration, les connaître par cœur permet de gagner un temps précieux lors d'examens ou de résolutions rapides de problèmes, et de fluidifier la compréhension des concepts plus avancés.

Q: Comment retenir les formules SOH CAH TOA ?

En français, on utilise souvent des acronymes comme "COSHYTADJ", "SINOPPOTTENOPPADJ" ou des phrases comme "cosadjip", "sinopip", "tanopadj" pour retenir que le Cosinus = Adjacent/Hypoténuse, le Sinus = Opposé/Hypoténuse, et la Tangente = Opposé/Adjacent.

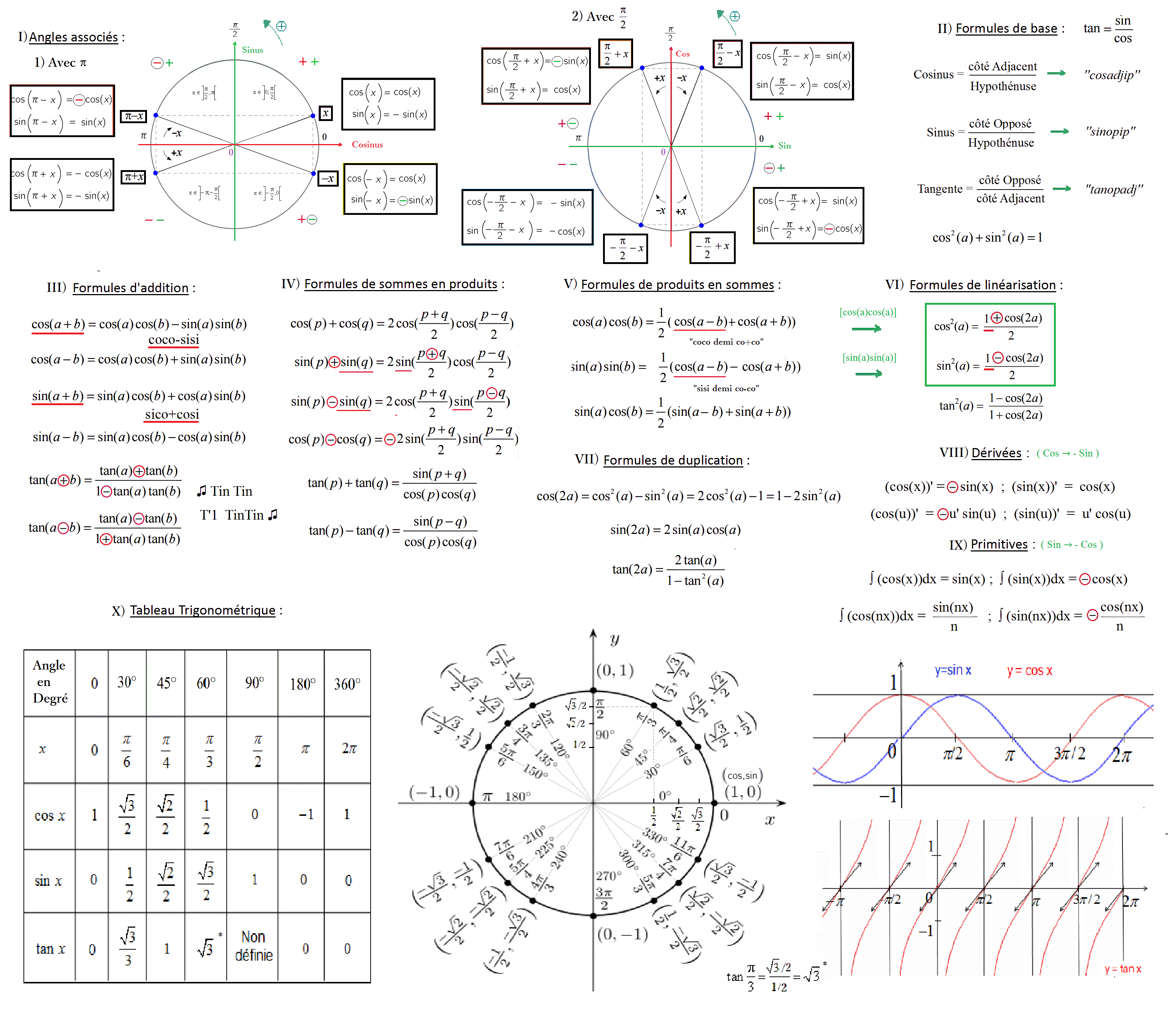
schéma récapitulatif des formules de trigonométrie — Schéma récapitulatif des principales formules de trigonométrie et astuces mnémotechniques. (Cliquez pour agrandir)

I) Angles associés : Le cercle trigonométrique, ton meilleur ami

Pour maîtriser les angles associés, le cercle trigonométrique est indispensable. Garde-le toujours en tête et n’hésite pas à le reproduire. Rappelle-toi que l’axe des abscisses (horizontal) correspond au cosinus et l’axe des ordonnées (vertical) au sinus.

1) Angles associés à pi (π)

Lorsque tu détermines les angles associés à pi, pars toujours de pi sur le cercle. Par exemple, pour cos(pi-x), tu pars de pi et tu « retires » x. En te situant dans l’intervalle ]pi/2 ; pi[, tu observes que le cosinus est négatif (car à gauche de l’axe des ordonnées) et le sinus est positif (car au-dessus de l’axe des abscisses). Ainsi, tu obtiens :

cos(pi – x) = – cos(x)
sin(pi – x) = + sin(x)
tan(pi – x) = – tan(x)

2) Angles associés à pi/2 (π/2)

Pour les angles associés à pi/2, l’astuce est de « permuter » les axes : cette fois-ci, l’axe des abscisses correspond au sinus et l’axe des ordonnées au cosinus. En prenant l’exemple de cos(pi/2 + x), tu commences de pi/2, puis tu « rajoutes » x. Tu te trouves alors dans l’intervalle ]pi/2 ; pi[. En appliquant la nouvelle correspondance des axes et en regardant les signes (sinus négatif et cosinus positif sur les axes « permutés »), tu as :

cos(pi/2 + x) = – sin(x)
sin(pi/2 + x) = + cos(x)
tan(pi/2 + x) = – cotan(x) ou -1/tan(x)

II) Formules de base : SOH CAH TOA à la française

Ces formules sont la base de la trigonométrie dans le triangle rectangle. Pour retenir les rapports entre les côtés, voici des astuces mnémotechniques efficaces :

Pour que le cosinus soit égal au côté Adjacent sur l’Hypoténuse, retiens « cosadjip » et prononce-le le plus rapidement possible ! (CAH en anglais)
De même, pour le sinus qui est égal au côté Opposé sur l’Hypoténuse, mémorise « sinopip » ! (SOH en anglais)
Enfin, pour la tangente qui est égal au côté Opposé sur le côté Adjacent, utilise « tanopadj » ! (TOA en anglais)

III) Formules d’addition : « Coco-sisi » et « Sico+cosi »

Les formules d’addition permettent de calculer le cosinus, le sinus ou la tangente de la somme ou de la différence de deux angles.

1) cos(a+b) et cos(a-b)

Pour cos(a+b) = cos(a)cos(b) – sin(a)sin(b), retiens « coco-sisi« . Le tiret entre « coco » et « sisi » symbolise le signe moins (-), pour ne pas le confondre avec le sinus.
Pour cos(a-b), il suffit d’inverser le signe : cos(a-b) = cos(a)cos(b) + sin(a)sin(b).

2) sin(a+b) et sin(a-b)

Pour sin(a+b) = sin(a)cos(b) + cos(a)sin(b), retiens « sico+cosi« . Ici, le signe (+) symbolise la symétrie entre sin()cos() et cos()sin(), ce qui t’aide à ne pas le confondre avec le cosinus.
Pour sin(a-b), il suffit d’inverser le signe : sin(a-b) = sin(a)cos(b) – cos(a)sin(b).

3) tan(a+b) et tan(a-b)

Pour tan(a+b) = (tan(a)+tan(b))/(1 – tan(a)tan(b)), tu peux retenir la mélodie ♫ « Tin Tin T’1 TinTin ! » ♫. Le signe (+) de tan(a+b) se retrouve au numérateur, tandis qu’un signe (-) apparaît au dénominateur.
Pour tan(a-b) = (tan(a)-tan(b))/(1 + tan(a)tan(b)), le signe (-) de tan(a-b) se retrouve au numérateur, tandis qu’un signe (+) apparaît au dénominateur.

IV) Formules de sommes en produits

Ces formules sont utiles pour transformer une somme ou une différence de sinus ou cosinus en un produit. Il est souvent plus facile de les visualiser sur le cercle trigonométrique.

sin(p) + sin(q) = 2sin((p+q)/2)cos((p-q)/2). Remarque que le signe (+) devant sin(q) se retrouve derrière le premier sin, après le 2.
sin(p) – sin(q) = 2cos((p+q)/2)sin((p-q)/2). Ici, le signe (-) devant sin(q) se retrouve derrière le second sin.
cos(p) + cos(q) = 2cos((p+q)/2)cos((p-q)/2).
cos(p) – cos(q) = -2sin((p+q)/2)sin((p-q)/2). C’est la seule formule à posséder un signe (-) devant. Pour t’en souvenir, pense que « cos(p) + cos(q) » est toujours « positif » (ils sont « contents » quand ils s’additionnent !), tandis qu’en soustraction, ils sont « malheureux », donc « négatifs » !

V) Formules de produits en sommes

Ces formules, souvent appelées « formules de linéarisation », transforment un produit de sinus ou cosinus en une somme. La visualisation sur le schéma principal est très utile pour cette section.

Pour retenir cos(a)cos(b) = (1/2)[cos(a-b)+cos(a+b)], utilise « coco demi co+co« .
Pour sin(a)sin(b) = (1/2)[cos(a-b)-cos(a+b)], retiens « sisi demi co-co« .
Pour sin(a)cos(b) = (1/2)[sin(a+b)+sin(a-b)], tu peux penser à « sico demi si+si« .

VI) Dérivées et Primitives trigonométriques : Le sens de rotation sur le cercle

Les dérivées et primitives des fonctions trigonométriques sont essentielles en analyse. Une astuce visuelle simple sur le cercle trigonométrique permet de les retenir sans effort :

Dérivées (sens horaire sur le cercle) :
- (cos(x))’ = – sin(x) : Imagine que « cosinus dérive (sur l’eau), il se cogne, perd sa tête (son ‘co’) et se transforme en sinus négatif ! »
- (sin(x))’ = cos(x)
Primitives (sens anti-horaire sur le cercle) :
- Intégrale de sin(x) dx = – cos(x) : « Lorsque sinus est intégré, il retrouve sa tête (son ‘co’) et se (re)transforme en cosinus négatif ! »
- Intégrale de cos(x) dx = sin(x)

Lien avec les angles associés à pi/2 et -pi/2

Il existe une astuce fascinante pour relier les dérivées/primitives aux formules d’angles associés à pi/2 :

Si tu connais tes dérivées :
- cos(pi/2 + x) = – sin(x) (ressemble à (cos(x))’ = -sin(x))
- sin(pi/2 + x) = cos(x) (ressemble à (sin(x))’ = cos(x))
Si tu connais tes primitives :
- sin(x – pi/2) = – cos(x) (ressemble à Intégrale de sin(x) dx = -cos(x))
- cos(x – pi/2) = sin(x) (ressemble à Intégrale de cos(x) dx = sin(x))

L’astuce pour ne pas confondre ? Dans le mot « dérivée », tu as le son « de » au début, comme le « 2 » de pi/2 (pi sur 2) et le « de » de « de plus (de +) » (pi/2 + x). Donc dérivée : (pi/2 + x) !

Dans le mot « primitive », tu as le « m » de « moins (-) ». Et si tu considères que la primitive est la suite de la dérivée, tu peux penser à (pi/2 + x – pi/2) pour arriver à (x – pi/2). Donc primitive : (x – pi/2) !

Ainsi, le fait de connaître ses dérivées permet aussi de connaître l’influence de (pi/2 + x) ; et connaître ses primitives permet aussi de connaître l’influence de (x – pi/2) !

VII) Tableau trigonométrique des valeurs remarquables

Le meilleur moyen de retenir les valeurs des angles remarquables (0, pi/6, pi/4, pi/3, pi/2, etc.) est de bien visualiser les courbes du sinus et du cosinus, ainsi que le cercle trigonométrique.

La fonction cosinus atteint son maximum de 1 lorsque l’angle est 0 : cos(0)=1.
La fonction sinus passe par zéro en étant croissante à l’origine : sin(0)=0. Tu peux imaginer cette courbe sinusoïdale est une vague qui mesure 1m hors de l’eau, puis 1m lorsqu’elle s’écrase au fond de l’eau, ainsi on obtient notre intervalle [-1; 1]. Et puisque le 0 correspond au milieu, ici, la surface de l’eau, on a sin(0)=0 & sin(pi)=0.

Pour déterminer les valeurs de la tangente dans le tableau, utilise simplement la formule fondamentale : tan = sin/cos !

Astuce bonus : cos(pi) et cos(pi/2)

cos(pi) = -1 : L’expression « cos (pi) » peut faire penser au terme « copie« . Si l’on copie sur son voisin, on risque d’avoir -1 sur sa note ! Donc cos(pi) = -1.
Pour se souvenir que cos(pi/2) = 0, on peut se dire que si l’on copie sur 2 voisins, cette fois-ci, on a 0 au contrôle !

Conclusion : La trigonométrie à portée de main !

Grâce à ces astuces mnémotechniques, la trigonométrie ne devrait plus être une source d’angoisse. En visualisant le cercle trigonométrique et en associant ces formules à des images ou des phrases clés, tu pourras les maîtriser et les appliquer rapidement, que ce soit pour tes cours, tes examens ou tes projets personnels.

N’oublie pas que la pratique est essentielle. Plus tu utiliseras ces astuces et résoudras des exercices, plus ces formules s’ancreront dans ta mémoire. Alors, à tes stylos et ton cercle trigonométrique : la trigonométrie n’aura bientôt plus de secrets pour toi !

Questions fréquentes sur les formules de trigonométrie (FAQ)

Pourquoi apprendre les formules de trigonométrie par cœur ?

Bien qu’il soit possible de les retrouver par démonstration, les connaître par cœur permet de gagner un temps précieux lors d’examens ou de résolutions rapides de problèmes, et de fluidifier la compréhension des concepts plus avancés.

Qu’est-ce que le cercle trigonométrique et à quoi sert-il ?

Le cercle trigonométrique est un cercle de rayon 1 centré à l’origine d’un repère orthonormé. Il sert à visualiser les fonctions sinus, cosinus, et tangente des angles, ainsi qu’à comprendre les relations entre les angles associés et les signes des fonctions trigonométriques dans les différents quadrants.

Comment retenir les formules SOH CAH TOA ?

En français, on utilise souvent des acronymes comme « COSHYTADJ », « SINOPPOTTENOPPADJ » ou des phrases comme « cosadjip », « sinopip », « tanopadj » pour retenir que le Cosinus = Adjacent/Hypoténuse, le Sinus = Opposé/Hypoténuse, et la Tangente = Opposé/Adjacent.

Quelle est la différence entre les formules d’addition et de transformation ?

Les formules d’addition (cos(a+b), sin(a+b)) permettent de développer des fonctions trigonométriques d’une somme ou différence d’angles. Les formules de transformation (sommes en produits et produits en sommes) servent à changer une somme/différence en produit, ou un produit en somme/différence, ce qui est utile pour simplifier des expressions ou résoudre des équations.

Comment ne pas se tromper avec les signes des dérivées et primitives de sinus/cosinus ?

On peut visualiser un cercle avec cos, -sin, -cos, sin dans le sens horaire. Pour les dérivées, on tourne dans le sens horaire (cos’ = -sin, (-sin)’ = -cos, etc.). Pour les primitives, on tourne dans le sens anti-horaire (Intégrale de cos = sin, Intégrale de sin = -cos, etc.).

La tangente est-elle toujours définie ?

Non, la fonction tangente n’est pas définie pour les angles où le cosinus est nul, c’est-à-dire pour pi/2 + k*pi, où k est un entier relatif. À ces valeurs, il y a des asymptotes verticales sur la courbe de la tangente.

Ces astuces sont-elles valables pour tous les niveaux ?

Ces astuces sont particulièrement utiles pour les lycéens et les étudiants en début de cycle supérieur, pour qui la mémorisation est un enjeu majeur. Elles peuvent aussi servir de rappel rapide pour des niveaux plus avancés.

Alors, tu l’as compris, l’ivresse des maths, et plus particulièrement de la trigonométrie, n’est plus un mythe ! En t’appropriant ces astuces mnémotechniques, tu n’apprends pas seulement des formules, tu t’ouvres une nouvelle perception de cette discipline. Laisse-toi emporter par cette fluidité retrouvée, et que chaque cosinus et sinus devienne une note dans ta propre symphonie mathématique. Enivre-toi de cette connaissance qui te libère du fardeau de la mémorisation brute, et continue de t’émerveiller devant la beauté des chiffres et des angles. Car, comme le disait le poète, il faut s’enivrer sans trêve, et aujourd’hui, c’est de trigonométrie que tu es ivre !