Cet article vous propose de comprendre, puis de mémoriser quatre théorèmes mathématiques fondamentaux en rapport avec les suites !
Mais.. qu’est ce qu’une suite ? En mathématiques, une suite est une famille d’éléments (appelés termes : U0, U1, U2, etc..).
Remarque : Plus rigoureusement, une suite réelle est une application de N (ensemble des entiers naturels (1,2,3)) à valeur dans R (ensemble des réels), et dont la notation indicielle est : (un)n ∈ N (cette suite est plus simplement notée (un)), avec l’élément Un qui est le terme général de cette suite. Attention à ne pas confondre les deux objets mathématiques : la suite (un) et terme général Un, qui ne signifient pas la même chose !
I) La plus simple des suites est celle des nombres pairs croissants : 2,4,6..
Remarque : Cette suite de nombres pairs est, en maths, une suite arithmétique de premier terme 0 et de raison 2. En effet, la définition d’une suite arithmétique est la suivante :
Où r correspond à la raison, U0 correspond au premier terme, Un correspond au terme principal, n et p correspondent à des indices (si n ≥ p ≥ n₀).
Concrètement, une suite arithmétique permet de décrire des phénomènes dont la variation est constante au cours du temps, comme l’évolution d’un compte bancaire non utilisé mais bénéficiant d’intérêts, ou encore l’évolution du niveau d’eau dans un verre si on laisse goutter le robinet au-dessus au même rythme.
Si l’on reprend l’exemple des nombres pairs croissants (2, 4, 6, ..), nous avons vu que c’était une suite arithmétique de premier terme 0 et de raison 2, c’est-à-dire : Un = n x 2 , donc U1 = 1 x 2 = 2 (premier terme est égal à 2), U2 = 2 x 2 = 4 , ainsi de suite !
II) Intuitivement, une suite possède une limite, cette limite est l’élément dont les termes de la suite se rapprochent le plus quand les indices deviennent très grands. Par exemple, la limite de la suite de chiffres (0 à 9) correspond au chiffre 9 (on dit que la suite converge vers 9), tandis que la limite des nombres pairs (2, 4, 6, etc..) est infinie (+∞) (on dit que la suite diverge).
Rappel : Les nombres sont représentés par une juxtaposition de chiffres (0 à 9), de même que les mots sont représentés par une juxtaposition de lettres.
III) Avant de passer aux théorèmes, il est important de maîtriser encore deux notions : la convergence (vers une limite) et la monotonie (croissance ou décroissance) d’une suite.
– Nous venons de voir les termes « convergence » et « divergence » dans la partie II), maintenant il est question d’en donner une définition rigoureuse :
Soit l ∈ R (l un réel), on dit que la suite (Un) converge vers l si et seulement si (ssi) :
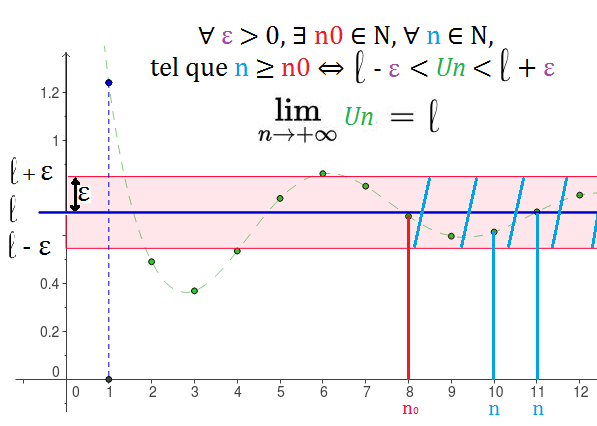
∀ ε > 0, ∃ n0 ∈ N, ∀ n ∈ N, tel que n ≥ n0 ⇔ l – ε < Un < l + ε , ce qui se note : 
Heureusement, cette définition d’apparence abjecte et complexe peut se représenter graphiquement, ce qui facilite grandement sa compréhension ! Pour revoir les notations et les quantificateurs (∃ : il existe, ∀ : quelque soit, ∈ : appartient, ε : epsilon une lettre grec), vous pouvez regarder l’introduction de cet article ICI).
– En ce qui concerne la monotonie :
Une suite (un) est croissante si le terme d’après est plus grand, c’est-à-dire si pour tout entier n, un ≤ un+1 (avec un+1 correspondant au terme après un ), pour déterminer une suite croissante par des calculs, il faut donc : un+1 − un ≥ 0.
Une suite (un) est décroissante si le terme d’après est plus petit, c’est-à-dire si pour tout entier n, un ≥ un+1 , pour déterminer une suite croissante par des calculs, il faut donc : un+1 − un ≤ 0.
Une suite (un) est monotone est croissante OU décroissante. Exemple : La suite ((-1)^n) n’est pas monotone, en effet cette suite est croissante ET décroissante, car celle-ci oscille entre 1 et (-1) !
Désormais, vous possédez un minimum de bases pour pouvoir assimiler et comprendre les quatre théorèmes qui vont suivre :
Théorème des gendarmes (ou d’encadrement) :
Dans les exercices, le théorème des gendarmes (ou d’encadrement) est utile lorsque la suite tend (converge) vers un réel l .
Théorème de comparaison :
Dans les exercices, le théorème de comparaison est utile lorsque la suite diverge vers +∞ ou -∞.
Théorème des suites monotones :
La borne supérieure (supremum ou sup) d’une partie d’un ensemble est le plus petit de ses majorants, tandis que la borne inférieure (infimum ou inf) d’une partie est le plus grand de ses minorants (voir ici la différence entre majorant et minorant).
Dans les exercices, le théorème des suites monotones est utile lorsque la suite est monotone, avant de l’utiliser, il faut voir s’il est possible de minorer ou de majorer la suite considérée.
Théorème des suites adjacentes :
Quelques astuces :
Pour ne plus confondre le théorème d’encadrement (des gendarmes) et le théorème de comparaison !
Il faut se dire que le théorème d’encadrement permet d’encadrer une valeur limite L ; dans le même ordre d’idée, des gendarmes peuvent encadrer un suspect afin de l’arrêter, cela permet de se souvenir que théorème des gendarmes = théorème d’encadrement !
De même, pour le théorème de comparaison, il faut se dire que les valeurs +∞ et -∞ peuvent être comparées (ce n’est pas très rigoureux de dire ça, mais c’est pour s’en souvenir), donc on utilise le théorème de comparaison uniquement quand l’une des suites diverge vers +∞ ou -∞ !
- Différence entre poulpe, pieuvre et calamar - 1 novembre 2021
- Différence entre Mitose et Méiose - 1 novembre 2021
- Les races de vache : les reconnaître - 17 septembre 2019
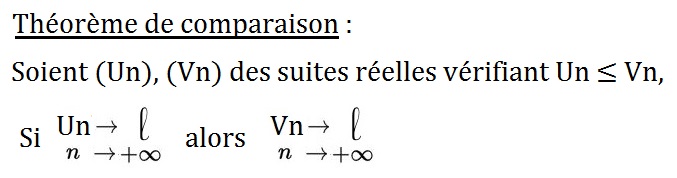
c’est vraiment cool et j’aimerais être abonné dans ce site, si possible.
Hello :)
Tu peux t’inscrire en cliquant sur « connexion », tout haut à gauche !
Au plaisir !
Je préfère de votre explication mrc