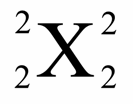Le problème du Phénix

Pour ce lundi énigme, il va falloir sortir la calculette !

Énoncé

Dans le carré latin ci-dessous, le nombre abcdef possède 6 chiffres et la propriété suivante: la ligne 2 est le nombre abcdef multiplié par 2, la ligne 3 est le nombre abcdef multiplié par 3, la ligne 4 est le nombre abcdef multiplié par 4, la ligne 5 est le nombre abcdef multiplié par 5 et la ligne 6 est le nombre abcdef multiplié par 6.
Par exemple, si abcdef = 123456, la deuxième ligne est 246912 (123456 x 2).

Qu’est-ce qu’un carré latin ?

Il s’agit d’une matrice dans laquelle chaque ligne et chaque colonne possède des chiffres différents et sans répétition, comme le Sudoku.

	a	b	c	d	e	f
× 2
× 3
× 4
× 5
× 6

Indice

Premier indice: pensez aux fractions.
Second indice: pensez aux nombres cycliques ! (Attention, cliquer sur le lien donne la réponse, donc si vous souhaitez réfléchir encore un peu, ne cliquez pas !)

Solution et explications

Il faut donc trouver un nombre qui se multiplie mais dont les chiffres qui le composent ne se répètent pas dans la même ligne et dans la même colonne.

Donc par essai erreur (ou par connaissance des nombres cycliques), on arrive à calculer en septièmes et à constater la manière dont se répètent les nombres:

1/7 = 0,142857 (abcdef)
2/7 = 0,285714
3/7 = 0,428571
4/7 = 0,571428
5/7 = 0,714285
6/7 = 0,857142

Intéressons-nous uniquement aux décimales: 142857 et ses multiples qui remplissent les conditions du carré latin !

	1	4	2	8	5	7
× 2	2	8	5	7	1	4
× 3	4	2	8	5	7	1
× 4	5	7	1	4	2	8
× 5	7	1	4	2	8	5
× 6	8	5	7	1	4	2

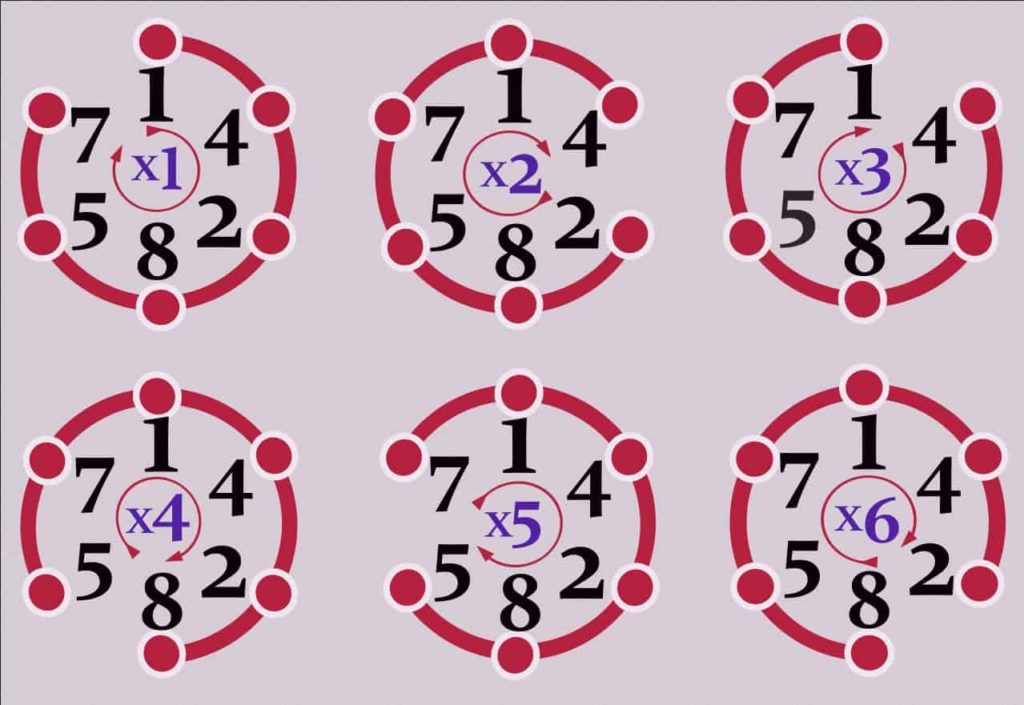
Et pour ce problème, il n’y a qu’une seule solution (dans l’optique où on ne permet pas que le nombre commence par un 0). Il faut trouver un nombre cyclique aussi appelé nombre phénix qui est un nombre entier naturel dont les permutations circulaires de ses chiffres correspondent aux multiples du nombre.
C’est la beauté des mathématiques et de ses nombres !

Observons cette infographie du nombre cyclique 142857 pour mieux saisir son fonctionnement: