Différence entre les opérateurs : Gradient ou Divergence ?

Nous avons vu dans plusieurs articles relatifs aux sciences (champ magnétique), des outils mathématiques comme le scalaire (défini par une valeur précise) et le vecteur (défini par trois éléments : le sens, la direction et la norme).

Nous allons désormais nous intéresser à deux nouveaux outils, le gradient et la divergence en coordonnées cartésiennes (x,y,z), (ces outils existent aussi en coordonnées cylindriques (r,θ,z) et sphériques (ρ,θ,φ), mais leur écriture est assez encombrante et ne permet pas forcément une bonne compréhension, contrairement aux coordonnées cartésiennes, définies seulement par (x,y,z)) .

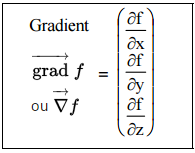
L’opérateur gradient (aussi appelé nabla) transforme un champ scalaire (f) en un champ vectoriel (la flèche du vecteur se trouve sur l’opérateur gradient) :

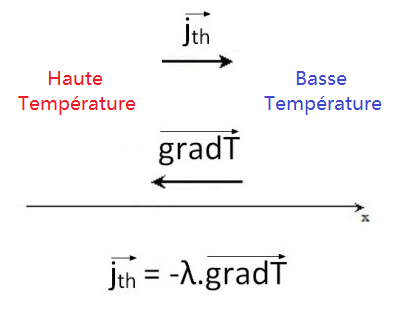
Remarque : Le vecteur gradient (de température, par exemple) se dirige du moins vers le plus, ainsi le vecteur densité de flux thermique se dirige du plus vers le moins. Cette relation est donnée par la loi de Fourier. Cette définition permet d’expliquer pourquoi lorsque la température à l’intérieur est plus élevée qu’à l’extérieur, on a une fuite de chaleur se dirigeant vers l’extérieur, vers l’environnement le plus froid.

Par ailleurs, le sens du gradient du moins vers le plus, s’applique aussi à des tensions, des concentrations ou encore des pressions, qui auront (pour les deux premières) respectivement un vecteur densité de courant de coulombs, et un de particules, donnés respectivement par la loi d’Ohm, et la loi de Fick.

L’opérateur divergence transforme un champ vectoriel (A) en un champ scalaire (la flèche du vecteur se trouve sur A, le champ vectoriel) :

Astuces :

On remarque que les termes « gradient » et « scalaire » possèdent tous les deux la lettre « a », ainsi on applique toujours le gradient sur un scalaire (gradient de température ou de pression).

On remarque aussi que les termes « divergence » et « vectoriel » possèdent tous les deux la lettre « v », ainsi on applique toujours la divergence sur un vecteur (divergence du champ magnétique ou de la vitesse).

Suppléments :

Il existe aussi deux autres types d’opérateurs mathématiques utiles :

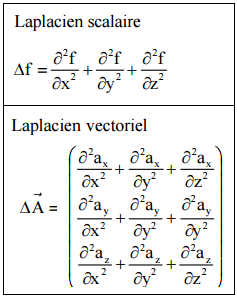
Le laplacien (scalaire) correspond à la divergence du gradient (d’un champ scalaire), le laplacien scalaire est aussi l’application au champ scalaire du carré de l’opérateur gradient (aussi appelé nabla), d’où les dérivées partielles secondes du laplacien.

Le rotationnel permet d’exprimer la tendance qu’ont les lignes de champ d’un champ vectoriel à tourner autour d’un point :

L’astuce consiste à mémoriser la ligne du milieu, en effet c’est la plus simple à visualiser car il y a une belle symétrie entre d(ax) au numérateur et dz au dénominateur ; la lettre « y » qui devrait se trouver au milieu n’y est pas !

Ensuite, une fois qu’on a l’image du d(ax) au dessus et dz en dessous (en rouge, pour la colonne de gauche, au milieu), il suffit d’inverser le sens dans la colonne de droite avec le signe moins ; puis, lorsque l’on descend, il suffit de continuer l’ordre des lettres x,y,z , en bleu, on passe de d(ax) à d(ay) (à gauche, en bas) ; de même à droite, on passe de d(az) à d(ax).

Dernier complément :

Le rotationnel du rotationnel correspond à la formule du découplage pouvant être utile lorsque l’on étudie les solutions des équations de Maxwell (qui feront aussi l’objet d’un prochain article pour les mémoriser à long terme).