Les formules de trigonométrie sont essentielles en maths, mais ce ne sont pas les seules ! Les dérivées et les primitives des fonctions cosinus et sinus sont aussi très utilisées (dans le domaine de la physique et des mathématiques) !
Quand on lit les formules des dérivées et des primitives, elles ont l’air simple comme ça ; mais elles le sont déjà moins quand il s’agit de les réécrire de mémoire ! La seule solution est de les apprendre par cœur, mais sans astuce, on a tendance à se tromper dans les signes ! C’est pourquoi JeRetiens vous propose une astuce mnémotechnique très imagée, mais aussi très efficace !
Dérivées :
La dérivée de cosinus est égale à un sinus négatif, et la dérivée de sinus est égale à un cosinus positif.
(cosinus)’ = – sinus ce qui donne : ( cos(x) )’ = – sin(x)
(sinus)’ = cosinus ce qui donne : ( sin(x) )’ = cos(x)
Astuce pour la Dérivée :
Pour l’astuce, on se concentre uniquement sur la dérivée de cosinus, car la dérivée de sinus est simple, il suffit de transformer le sinus en cosinus. Donc pour la dérivée de cosinus, il faut imaginer l’histoire suivante :
Lorsque COSINUS dérive (sur l’eau), il se cogne (contre un tronc d’arbre), perd sa tête (son « CO ») et se transforme en SINUS négatif (Négatif car il n’est pas content d’avoir perdu sa tête) !
Primitives (Intégrations) :
La primitive (sans borne) de cosinus est égale à un sinus positif, et la primitive de sinus est égale à un cosinus négatif.
∫(cosinus) = sinus ce qui donne : ∫( cos(x) )dx = sin(x)
∫(sinus) = – cosinus ce qui donne : ∫( sin(x) )dx = – cos(x)
Astuce pour l’Intégration (primitive) :
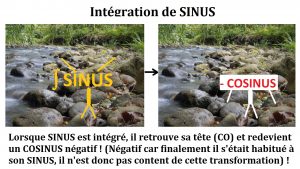
Il faut s’imaginer être dans la même histoire, mais cette fois-ci la scène se passe au moment où SINUS est arrivé sur la terre ferme (il est positif et content d’être sorti de l’eau) ! Maintenant qu’il est sans danger, on lui remet sa tête (on l’intègre) !
Lorsque SINUS est intégré, il retrouve sa tête (son « CO ») et se (re)transforme en COSINUS négatif ! (Négatif car finalement il s’était habitué à son SINUS, et n’est pas content de cette transformation) !
- Les trois singes de la sagesse : Mizaru, Kikazaru, Iwazaru - 18 décembre 2025
- Pâte brisée, sablée ou feuilletée ? - 11 décembre 2025
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
Rejoignez-nous sur Instagram !
Découvrez nos infographies et astuces : @JeRetiensNet


Il ne me semble pas que ces « astuces » soient très judicieuses. Il est préférable de se placer sur le cercle trigonométrique et de réfléchir, sachant qu’une dérivée positive veut dire que la fonction est croissante et une dérivée négative veut dire qu’elle est décroissante.
Ainsi, en se déplaçant sur le premier quart du cercle, les valeurs de sinus augmentent, sa dérivée doit donc être positive et en effet, cos x, sur ce premier quart de cercle renvoie des valeurs positives. A l’inverse, toujours en se déplaçant dans ce premier quart de cercle, les valeurs de cosinus diminuent, sa dérivée doit donc être négative et en effet -sin x renvoie une valeur négative !
On peut faire la même chose pour le deuxième quart de cercle : En se déplaçant sur ce quart, les valeurs sinus diminuent donc sa dérivée doit être négative, ce qui est le cas de cos x dans ce quart. Les valeurs de cosinus diminuent également et ça tombe bien car la valeur renvoyée par – sin x est négative !
Pour le troisième quart de cercle, les valeurs sinus continuent à diminuer et sa tombe bien car la dérivée cos x dans ce troisième quart est négative ! A l’inverse, sur ce quart, les valeurs cosinus augmentent et la dérivée, – sin x, renvoie des valeurs positives !
Enfin pour le quatrième quart, les valeurs de sinus et cosinus augmentent, leurs dérivées doivent être positives. Ce qui est le cas de cos x (la dérivée de sin x) et de -sin x (la dérivée de cos x) !
bjr linel
tu es dur.. les astuces c’est très personnel, donc tes astuces sont bien, celles d’adrien aussi, et selon la perspective du lecteur les unes ou les autres seront plus pertinentes voilà tout
amicalement
Merci pour ces astuces plutôt originales qui fonctionnent (selon moi en tout cas), je les proposerai a mes élèves dès la rentrée !