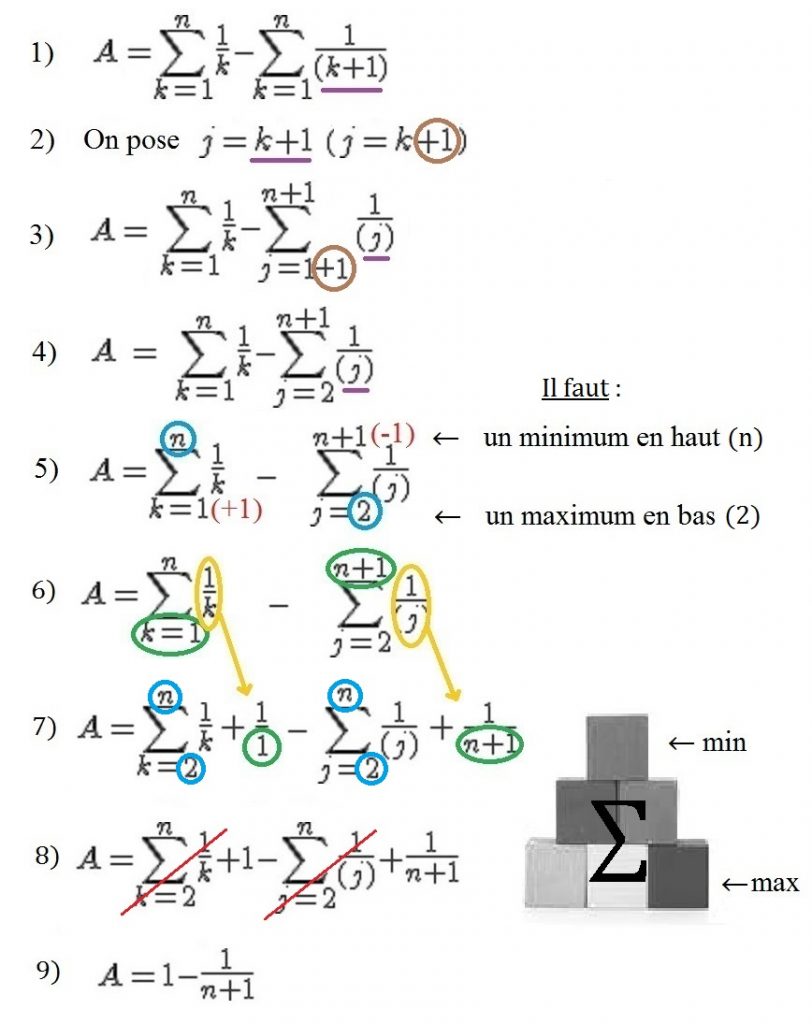
Calculs de sommes (∑) avec changements d’indices

Les calculs de sommes faisant intervenir des changements d’indices sont très utiles en maths (études supérieures), car ils permettent de transformer une lourde expression en un résultat plus concis et donc plus facile à interpréter mathématiquement.

Pour faire ce genre de calculs, il faut bien comprendre les raisonnements qui s’enchaînent ; cependant, cette méthode de calcul n’est pour le moins pas naturelle et assez abstraite, c’est pourquoi, dans cet article, nous vous proposons une astuce mnémotechnique pour pouvoir calculer ces sommes sans trop de soucis, et pour que le placement des nombreux termes ne vous pose pas (ou plus) de problème !

Astuce :

L’astuce que nous vous proposons consiste à imaginer la somme ∑ (sigma) comme étant une pyramide.

Il faut penser à une pyramide car dans l’étape 7 (ci-dessous) il est question de répartir les valeurs du bas et du haut, en effet, les valeurs les plus élevées doivent se trouver en bas de la somme (∑), tandis que les valeurs les moins élevées doivent se trouver en haut de la somme (∑) ; comme pour une pyramide, celle-ci ne peut tenir que si le bas est solide (si les blocs sont nombreux) !

C’est pourquoi, dans l’étape 7, on retrouve (entourés en bleu) les nombres « 2 » en bas (plus grand que 1), et les nombres « n » en haut (plus petit que (n+1)) !

L’exemple ci-dessous correspond à la soustraction de deux sommes (∑(1/k) – ∑(1/(k+1))) sur laquelle il va falloir changer les indices :

Dans l’étape 1, il faut se débarrasser du terme encombrant (1/k+1), on le remplace donc dans l’étape 2 par (1/j) qui ressemble à (1/k) et que l’on pourra annuler lors de l’étape 9 !

Dans l’étape 3, on réalise l’addition suivante : j = 1 (+ 1) , le deuxième 1 provient du changement de variable j = k + 1.

Dans l’étape 5, il faut que les termes en haut de la somme soient les moins élevés, tandis qu’en bas, il faut qu’ils soient les plus élevés, comme pour une pyramide !

L’étape 6 est la continuité de l’étape 5, elle nous montre que le fait d‘ajouter 1 en bas pour obtenir 2 et que de soustraire 1 en haut pour obtenir n, engendre un calcul de sommes, dans lequel les termes entourés en jaune doivent être additionnés à la somme correspondante (+1/k pour la première somme, et +1/j pour la deuxième), ensuite le 1/k de la première somme et le 1/j de la deuxième doivent être remplacés par les termes entourés en vert, on obtient ainsi 1/1 et 1/(n+1).

Puisque les variables k et j sont muettes (on peut les remplacer par n’importe quelle autre variable), cela nous permet de réaliser l’étape 8, c’est-à-dire d’annuler les termes (en les soustrayant), afin d’obtenir le résultat final dans l’étape 9 !

J’espère que cet article vous a été utile ; en tout cas, si vous avez besoin d’une astuce sur des formules, des dates ou autres, n’hésitez pas à nous demander : ICI !