Les calculs de sommes avec changements d’indices représentent l’un des outils les plus puissants en mathématiques supérieures, particulièrement en analyse, en algèbre et en théorie des probabilités. Ces techniques permettent de transformer des expressions mathématiques complexes et lourdes en résultats concis, élégants et plus facilement interprétables. Elles interviennent dans de nombreux domaines : développements en séries, démonstrations par récurrence, calculs de limites, transformations de Fourier, et bien d’autres applications fondamentales.
Cependant, la manipulation des indices de sommation n’est pas intuitive pour la plupart des étudiants. Le raisonnement abstrait nécessaire, la gestion simultanée de plusieurs variables, et la nécessité de maintenir la cohérence lors des transformations rendent ces calculs particulièrement délicats. Les erreurs de placement des bornes, la confusion entre les indices, ou l’oubli de termes compensatoires sont des pièges fréquents. C’est pourquoi cet article vous propose une méthode mnémotechnique visuelle basée sur l’image d’une pyramide, ainsi qu’un guide détaillé étape par étape pour maîtriser ces calculs essentiels.
En bref
Les calculs de sommes avec changements d’indices permettent de transformer des expressions mathématiques complexes en résultats concis. L’astuce mnémotechnique fondamentale consiste à imaginer le symbole de sommation ∑ (sigma) comme une pyramide : les valeurs les plus élevées doivent se trouver en bas de la somme (base solide de la pyramide), tandis que les valeurs les moins élevées doivent se trouver en haut (sommet). Par exemple, si k va de 1 à n, après changement d’indice j = k+1, les nouvelles bornes deviennent j = 2 (en bas, plus grand) et j = n+1 (en haut). La méthode en 9 étapes permet de calculer des différences de sommes comme ∑(1/k) – ∑(1/(k+1)) : 1) remplacer le terme encombrant, 2) introduire une nouvelle variable j, 3) calculer les nouvelles bornes, 4-7) ajuster les bornes selon le principe de la pyramide, 8-9) exploiter le caractère muet des variables pour annuler les termes identiques. Cette technique s’applique aux séries télescopiques, aux démonstrations par récurrence et à de nombreux calculs d’analyse.
Contexte mathématique : les sommes et leurs notations
Définition de la notation sigma (∑)
La notation sigma (∑) est une convention mathématique introduite par Leonhard Euler au XVIIIe siècle pour représenter de manière compacte la somme d’une suite de termes. Elle se note :
∑k=ab f(k)
Cette notation signifie : additionner tous les termes f(k) lorsque k prend successivement toutes les valeurs entières de a (borne inférieure) à b (borne supérieure). Formellement :
∑k=ab f(k) = f(a) + f(a+1) + f(a+2) + … + f(b-1) + f(b)
Par exemple, ∑k=14 k² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30
Importance des changements d’indices
Les changements d’indices (ou changements de variables) sont essentiels pour plusieurs raisons :
- Simplification d’expressions : transformer une somme complexe en une forme plus maniable
- Identification de motifs : révéler des structures cachées comme les séries télescopiques
- Démonstrations : permettre des preuves par récurrence ou des manipulations algébriques
- Changement de variable d’intégration : analogie avec les substitutions en calcul intégral
- Unification de termes : rassembler des sommes ayant des indices différents
Variables muettes et leur importance
Un concept fondamental est celui de variable muette (ou variable liée). L’indice de sommation k dans ∑k=1n f(k) est une variable muette : elle n’a de signification qu’à l’intérieur de la somme et peut être remplacée par n’importe quelle autre lettre sans changer le résultat.
Par exemple : ∑k=1n k² = ∑j=1n j² = ∑i=1n i²
Cette propriété est cruciale car elle permet de manipuler les sommes, de les comparer et de les combiner, comme nous le verrons dans la méthode détaillée.
L’astuce mnémotechnique de la pyramide
Principe visuel : imaginer ∑ comme une pyramide
L’astuce fondamentale proposée dans cet article consiste à imaginer le symbole de sommation ∑ (sigma) comme une pyramide. Cette visualisation aide à se rappeler la règle essentielle du placement des bornes lors d’un changement d’indices.
Tout comme une pyramide ne peut tenir que si sa base est solide et large (avec de nombreux blocs lourds), tandis que son sommet est léger et étroit, les sommes doivent respecter la même logique :
- En bas du sigma (∑) : placer les valeurs les plus ÉLEVÉES (base large et solide)
- En haut du sigma (∑) : placer les valeurs les moins ÉLEVÉES (sommet étroit et léger)
Application pratique de l’analogie
Prenons un exemple concret. Si nous effectuons le changement d’indice j = k + 1, et que k varie initialement de 1 à n, alors :
- Lorsque k = 1 (valeur minimale), alors j = 1 + 1 = 2
- Lorsque k = n (valeur maximale), alors j = n + 1
En appliquant le principe de la pyramide :
- En bas : on place 2 (valeur élevée par rapport à 1)
- En haut : on place n+1 (mais attention, si n+1 > 2, il faut ajuster, comme expliqué dans la méthode détaillée)
L’image de la pyramide rappelle visuellement que la borne inférieure (base) doit être plus petite numériquement que la borne supérieure (sommet), ce qui peut sembler contre-intuitif puisqu’on parle de « valeurs élevées » pour la base. Plus précisément : la borne inférieure est celle qui vient en premier dans l’ordre croissant (elle commence la sommation), et la borne supérieure termine la sommation.
Pourquoi cette analogie fonctionne-t-elle ?
L’analogie de la pyramide fonctionne parce qu’elle encode visuellement deux informations essentielles :
- Ordre naturel : Dans une sommation, on additionne de la plus petite valeur à la plus grande (de bas en haut dans la pyramide)
- Stabilité structurelle : La borne inférieure (nombreuse, solide) supporte toute la somme, tandis que la borne supérieure (unique, légère) la termine
Cette métaphore visuelle transforme une règle abstraite en image concrète, facilitant grandement la mémorisation et l’application correcte lors des calculs.
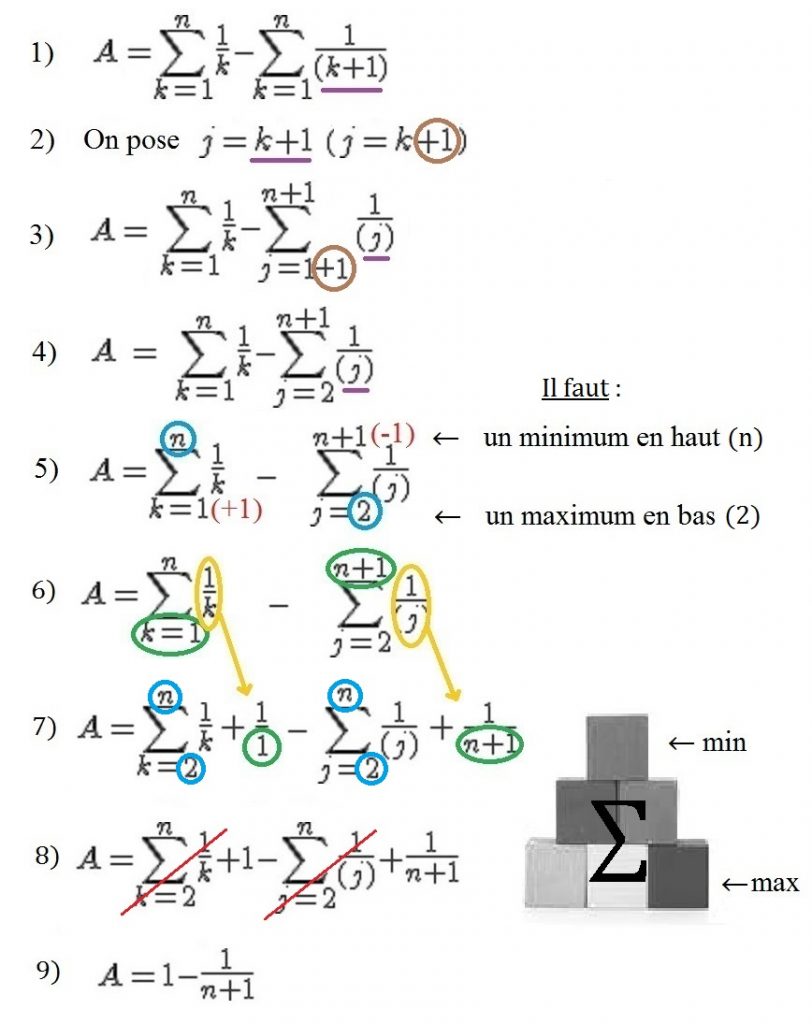
Méthode détaillée en 9 étapes : exemple complet
Problème initial
Nous allons calculer la différence de deux sommes avec changement d’indices :
∑k=1n (1/k) – ∑k=1n (1/(k+1))
Cette expression représente une série télescopique, type d’expression qui, après manipulation appropriée, voit la plupart de ses termes s’annuler mutuellement, laissant un résultat simple.
Étape 1 : Identifier le terme encombrant
Le terme 1/(k+1) dans la deuxième somme est « encombrant » car il diffère de 1/k dans la première somme. L’objectif est de le remplacer par une expression qui ressemblera davantage à 1/k afin de pouvoir éventuellement simplifier ou annuler des termes.
Stratégie : Effectuer un changement de variable pour transformer 1/(k+1) en une forme similaire à 1/k.
Étape 2 : Introduire une nouvelle variable j
Posons le changement de variable : j = k + 1
Alors : k = j – 1, et donc 1/(k+1) = 1/j
La deuxième somme devient :
∑k=1n (1/(k+1)) = ∑j=?? (1/j)
Il reste à déterminer les nouvelles bornes pour j.
Étape 3 : Calculer les nouvelles bornes
Puisque j = k + 1 :
- Lorsque k = 1 (borne inférieure initiale), alors j = 1 + 1 = 2
- Lorsque k = n (borne supérieure initiale), alors j = n + 1 = n+1
La deuxième somme s’écrit maintenant :
∑j=2n+1 (1/j)
Étape 4 : Expression complète après changement de variable
Notre expression devient :
∑k=1n (1/k) – ∑j=2n+1 (1/j)
Nous avons maintenant deux sommes avec des bornes différentes. Pour les comparer et potentiellement annuler des termes, nous devons harmoniser les bornes.
Étape 5 : Appliquer le principe de la pyramide
Selon le principe de la pyramide, nous voulons que :
- Les bornes inférieures soient identiques (même base)
- Les bornes supérieures soient identiques (même sommet)
Actuellement :
- Première somme : de 1 à n
- Deuxième somme : de 2 à n+1
Objectif : uniformiser à « de 2 à n ».
Étape 6 : Ajuster les bornes et extraire les termes compensatoires
Pour la première somme, passer de k=1 à k=2 comme borne inférieure signifie retirer le premier terme (k=1) :
∑k=1n (1/k) = 1/1 + ∑k=2n (1/k)
Pour la deuxième somme, passer de j=n+1 à j=n comme borne supérieure signifie retirer le dernier terme (j=n+1) :
∑j=2n+1 (1/j) = ∑j=2n (1/j) + 1/(n+1)
Étape 7 : Vérification du principe de la pyramide
Nos deux sommes ont maintenant les mêmes bornes (de 2 à n), conformément au principe de la pyramide :
- En bas : valeur 2 (borne inférieure, plus petite)
- En haut : valeur n (borne supérieure, plus grande)
L’expression complète devient :
[1/1 + ∑k=2n (1/k)] – [∑j=2n (1/j) + 1/(n+1)]
Étape 8 : Exploiter le caractère muet des variables
Puisque k et j sont des variables muettes, nous pouvons écrire :
∑k=2n (1/k) = ∑j=2n (1/j)
Ces deux sommes sont identiques ! Elles représentent exactement la même addition :
1/2 + 1/3 + 1/4 + … + 1/n
Étape 9 : Simplification finale et résultat
En distribuant le signe moins et en annulant les termes identiques :
1/1 + ∑k=2n (1/k) – ∑j=2n (1/j) – 1/(n+1)
= 1/1 + ∑k=2n (1/k) – ∑j=2n (1/j) – 1/(n+1)
= 1 – 1/(n+1)
Ce résultat élégant montre que tous les termes intermédiaires se sont annulés (caractéristique des séries télescopiques), ne laissant que le premier terme de la première somme et le dernier terme de la deuxième.
Applications des changements d’indices
Séries télescopiques
Les séries télescopiques sont des sommes où la plupart des termes s’annulent mutuellement, comme un télescope qui se replie sur lui-même. L’exemple que nous venons de traiter en est une illustration parfaite. Ces séries apparaissent fréquemment dans :
- Les démonstrations de formules de sommes (comme la somme des n premiers entiers)
- Le calcul de limites de suites définies par des sommes
- L’évaluation de certaines intégrales par méthode de Riemann
Démonstrations par récurrence
Les changements d’indices interviennent souvent dans les preuves par récurrence, notamment pour :
- Passer de l’hypothèse de récurrence à n à la propriété à n+1
- Réindexer une somme pour faire apparaître l’hypothèse de récurrence
- Simplifier l’expression à démontrer en isolant certains termes
Développements en séries
Dans l’étude des séries entières, des séries de Fourier ou des développements de Taylor, les changements d’indices permettent de :
- Identifier des motifs récurrents
- Regrouper des termes similaires
- Démontrer des relations entre différentes séries
- Calculer des coefficients par identification
Transformations et convolutions
En analyse de Fourier, en traitement du signal et en probabilités, les changements d’indices sont essentiels pour :
- Calculer des produits de convolution
- Effectuer des changements de variable dans les transformées
- Manipuler des sommes doubles ou multiples
Erreurs courantes et pièges à éviter
Erreur 1 : Oublier d’ajuster les bornes
L’erreur la plus fréquente consiste à changer la variable dans le terme général sans modifier les bornes en conséquence. Si j = k + 1 et que k va de 1 à n, on ne peut pas écrire que j va aussi de 1 à n !
Règle : Toujours calculer explicitement les nouvelles bornes en substituant les valeurs extrêmes de l’ancienne variable.
Erreur 2 : Inverser les bornes
Placer la valeur la plus grande en bas et la plus petite en haut invalide la somme. C’est précisément pour éviter cette erreur que l’astuce de la pyramide a été développée.
Vérification : La borne inférieure doit toujours être numériquement inférieure ou égale à la borne supérieure.
Erreur 3 : Confusion entre variables muettes et variables libres
Dans l’expression ∑k=1n k², k est muette mais n est libre (elle dépend du contexte). On peut remplacer k par j, mais pas n arbitrairement.
Distinction : Les variables muettes apparaissent dans les bornes ET dans le terme général ; les variables libres apparaissent seulement dans les bornes.
Erreur 4 : Négliger les termes compensatoires
Lors de l’ajustement des bornes (étape 6), oublier d’extraire les termes ajoutés ou retirés conduit à des résultats faux.
Vigilance : Chaque modification de borne génère un terme qu’il faut explicitement ajouter ou soustraire.
Conseils pratiques pour maîtriser la technique
Conseil 1 : Visualiser la pyramide systématiquement
Avant d’écrire les nouvelles bornes, dessinez mentalement (ou sur papier) une pyramide et demandez-vous : « Quelle valeur doit être en bas (base solide) et quelle valeur doit être en haut (sommet) ? »
Conseil 2 : Détailler chaque étape
Ne sautez pas d’étapes dans vos calculs, surtout au début. Écrivez explicitement le changement de variable, calculez les nouvelles bornes, extrayez les termes compensatoires. Avec la pratique, vous pourrez condenser certaines étapes.
Conseil 3 : Vérifier avec des cas particuliers
Testez votre résultat avec de petites valeurs de n. Par exemple, avec n=3, développez explicitement les deux sommes avant et après transformation, et vérifiez que vous obtenez le même résultat numérique.
Conseil 4 : Pratiquer avec différents types de changements
Les changements d’indices ne se limitent pas à j = k+1. Entraînez-vous avec :
- j = k – 2 (décalage négatif)
- j = 2k (multiplication)
- j = n – k (inversion)
- j = k² (transformations non linéaires, plus rares)
Conseil 5 : Maîtriser les propriétés des sommes
Réviser les propriétés fondamentales :
- Linéarité : ∑(a·f(k) + b·g(k)) = a·∑f(k) + b·∑g(k)
- Découpage : ∑k=ab f(k) = ∑k=ac f(k) + ∑k=c+1b f(k)
- Extraction de constantes : ∑k=ab C = C·(b-a+1)
Conclusion : de l’abstraction à la maîtrise
Les calculs de sommes avec changements d’indices représentent une compétence essentielle en mathématiques supérieures, indispensable dans de nombreux domaines de l’analyse, de l’algèbre et des probabilités. Bien que ces manipulations puissent sembler abstraites et contre-intuitives au premier abord, la méthode structurée présentée dans cet article, couplée à l’astuce mnémotechnique de la pyramide, offre un cadre solide pour aborder ces calculs avec confiance.
L’image de la pyramide – base large et solide en bas (valeurs élevées), sommet étroit en haut (valeurs réduites) – fournit un repère visuel immédiat pour placer correctement les bornes après un changement d’indices. Cette métaphore transforme une règle formelle abstraite en une image concrète et mémorable, réduisant considérablement les erreurs de placement et facilitant l’apprentissage.
La méthode détaillée en 9 étapes décompose le processus complet : identification du terme problématique, introduction d’une nouvelle variable, calcul des nouvelles bornes, application du principe de la pyramide, ajustement avec extraction des termes compensatoires, exploitation du caractère muet des variables, et simplification finale. Chaque étape a sa logique propre et contribue à la transformation progressive d’une expression complexe en un résultat élégant.
L’exemple traité – le calcul de ∑(1/k) – ∑(1/(k+1)) aboutissant à 1 – 1/(n+1) – illustre parfaitement le pouvoir des séries télescopiques où l’annulation de termes intermédiaires révèle une structure cachée. Ce type de calcul apparaît constamment dans les démonstrations mathématiques, les calculs de limites, et l’étude de convergence de suites définies récursivement.
Au-delà de la technique pure, comprendre les changements d’indices développe une intuition mathématique plus profonde sur la nature des variables muettes, l’équivalence de représentations différentes d’un même objet mathématique, et la flexibilité des notations. Ces compétences transcendent les sommes finies et s’appliquent aux intégrales, aux séries infinies, aux transformées et à de nombreux autres domaines mathématiques avancés.
La maîtrise de cette technique nécessite pratique et patience. Ne vous découragez pas face aux difficultés initiales : commencez par des exemples simples, détaillez chaque étape, vérifiez vos résultats avec des cas particuliers, et progressivement, ces manipulations deviendront naturelles. Avec le temps, vous reconnaîtrez instantanément les situations où un changement d’indice simplifiera l’expression, et vous effectuerez ces transformations avec fluidité et confiance.
Les mathématiques supérieures demandent de développer une boîte à outils de techniques et d’astuces. Les changements d’indices, avec l’aide de la pyramide mnémotechnique, constituent un outil puissant que vous utiliserez tout au long de vos études et au-delà. Maîtrisez cette technique, et vous découvrirez qu’elle transforme des calculs apparemment insurmontables en exercices élégants et instructifs.
Questions fréquentes sur les changements d’indices
Qu’est-ce qu’un changement d’indice dans une somme ?
Un changement d’indice (ou changement de variable) consiste à remplacer la variable de sommation par une autre variable reliée à la première par une relation mathématique. Par exemple, si on a ∑k=1n f(k+1) et qu’on pose j = k+1, la somme devient ∑j=2n+1 f(j). Cette technique permet de transformer des expressions complexes en formes plus simples, de révéler des structures cachées, ou d’unifier plusieurs sommes ayant des indices différents. Les bornes doivent être recalculées en fonction de la nouvelle variable pour préserver la validité mathématique de l’expression.
Comment retenir où placer les bornes après un changement d’indice ?
L’astuce mnémotechnique de la pyramide est très efficace : imaginez le symbole ∑ (sigma) comme une pyramide. Les valeurs les plus élevées (bornes supérieures) doivent se trouver en bas de la somme (base solide de la pyramide), et les valeurs les moins élevées (bornes inférieures) en haut (sommet de la pyramide). Plus concrètement, calculez les nouvelles bornes en substituant : si j = k+1 et k va de 1 à n, alors quand k=1, j=2 (borne inférieure), et quand k=n, j=n+1 (borne supérieure). Vérifiez toujours que borne inférieure ≤ borne supérieure.
Qu’est-ce qu’une variable muette dans une somme ?
Une variable muette (ou variable liée) est l’indice de sommation qui n’a de signification qu’à l’intérieur de la somme et peut être remplacé par n’importe quelle autre lettre sans changer le résultat. Par exemple, ∑k=1n k² = ∑j=1n j² = ∑i=1n i² représentent exactement la même somme (1² + 2² + … + n²). Cette propriété est cruciale pour comparer et annuler des termes dans des calculs impliquant plusieurs sommes. À l’inverse, n est une variable libre qui dépend du contexte et ne peut pas être changée arbitrairement.
Qu’est-ce qu’une série télescopique ?
Une série télescopique est une somme où la plupart des termes s’annulent mutuellement, ne laissant que quelques termes aux extrémités, comme un télescope qui se replie. L’exemple ∑k=1n (1/k – 1/(k+1)) se développe en (1/1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + … + (1/n – 1/(n+1)), où tous les termes intermédiaires s’annulent, ne laissant que 1/1 – 1/(n+1) = 1 – 1/(n+1). Ces séries sont fréquentes en analyse et permettent de calculer des sommes qui sembleraient autrement très complexes. Les changements d’indices révèlent souvent cette structure télescopique.
Comment vérifier qu’un changement d’indice est correct ?
Pour vérifier un changement d’indice, utilisez plusieurs méthodes : 1) Développez explicitement les premiers et derniers termes de la somme originale et de la somme transformée pour vérifier qu’ils sont identiques. 2) Testez avec une petite valeur numérique (n=3 ou n=4) et calculez la somme avant et après transformation. 3) Vérifiez que les nouvelles bornes satisfont : borne inférieure ≤ borne supérieure. 4) Assurez-vous que tous les termes compensatoires ont été correctement extraits lors de l’ajustement des bornes. 5) Utilisez le principe de la pyramide pour vérifier le placement des bornes.
Quand doit-on effectuer un changement d’indice ?
Un changement d’indice est utile dans plusieurs situations : 1) Lorsqu’on veut unifier plusieurs sommes ayant des indices différents pour les comparer ou les combiner. 2) Pour révéler une structure télescopique cachée. 3) Dans les démonstrations par récurrence, pour faire apparaître l’hypothèse de récurrence. 4) Pour simplifier des expressions où l’indice apparaît dans des formes complexes (k+1, 2k, n-k). 5) Pour calculer des produits de convolution. 6) Lors de l’identification de coefficients dans des développements en série. Avec l’expérience, vous reconnaîtrez rapidement les situations où un changement d’indice simplifiera le problème.
Pourquoi extrait-on des termes lors de l’ajustement des bornes ?
Lorsqu’on modifie les bornes d’une somme (par exemple, passer de k=1 à k=2), on change effectivement les termes qui sont additionnés. Pour compenser ce changement et préserver l’égalité mathématique, il faut extraire explicitement les termes ajoutés ou retirés. Si on passe de ∑k=1n f(k) à ∑k=2n f(k), on a retiré le terme f(1), donc on doit écrire : ∑k=1n f(k) = f(1) + ∑k=2n f(k). Ces termes compensatoires sont essentiels pour obtenir le résultat correct, comme dans l’étape 6 de la méthode détaillée.
Peut-on faire des changements d’indice avec des sommes infinies ?
Oui, les changements d’indice s’appliquent également aux séries infinies (∑k=1∞ f(k)), mais avec des précautions supplémentaires. Il faut s’assurer que la série converge avant et après le changement d’indice, et que les manipulations préservent cette convergence. Les mêmes principes s’appliquent (calculer les nouvelles bornes, extraire les termes compensatoires si nécessaire), mais la borne supérieure reste l’infini. Le caractère muet des variables et l’astuce de la pyramide restent valables. Ces techniques sont fondamentales dans l’étude des séries entières, des séries de Fourier, et des développements asymptotiques.
- Les trois singes de la sagesse : Mizaru, Kikazaru, Iwazaru - 18 décembre 2025
- Pâte brisée, sablée ou feuilletée ? - 11 décembre 2025
- Différence entre poulpe, pieuvre et calamar - 18 mars 2025
Rejoignez-nous sur Instagram !
Découvrez nos infographies et astuces : @JeRetiensNet

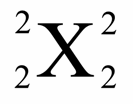
salut
nos aurions pu résoudre tout de suite cette somme car elle est télescopique