Les développements limités (DL) sont employés en maths (pour déterminer la convergence d’une suite) et en physique (pour remplacer l’expression d’une fonction compliquée par une fonction approchée, plus facile à exploiter).
Voici une fiche des développement limités (au voisinage de 0) les plus utilisés :
Pour une question de place, nous avons décidé de ne pas mettre les fonctions hyperboliques dans ce tableau, car ce sont les mêmes que les fonctions cosinus et sinus, avec uniquement des symboles (+) à la place des symboles (-).
Les astuces qui vont suivre ne concernent uniquement les premiers termes (à droite de la fiche), en effet, lors d’un exercice ou d’une approximation de courbe, ce sont généralement les premiers termes des DL que l’on utilise, et non l’ordre n.
Remarque : Il est possible de retrouver les premiers termes de ces fonctions avec la formule de Taylor-Young, cependant il est plus aisé et rapide de se souvenir directement des développements usuels lors d’un examen où le temps est limité, par exemple.
Astuces :
Après avoir observé ces DL pendant des heures, on a finalement réussi à trouver des points communs entre toutes ces relations, ce qui peut faciliter leur apprentissage !
Tout d’abord, cela n’est pas précisé sur la fiche ci-dessus, mais pour l’astuce, il est nécessaire expliciter le nom des fonctions :
cos(x) correspond à la fonction cosinus, sin(x) à la fonction sinus, ch(x) à la fonction cosinus hyperbolique, sh(x) à la fonction sinus hyperbolique, ex correspond à la fonction exponentielle, ln(1+x) correspond à une fonction logarithme, 1/(1+x) à la fonction « fraction positive », 1/(1-x) à la fonction « fraction négative », √(1+x) correspond à la fonction racine carrée et enfin, √(1/(1+x)) à la fonction « fraction racine carrée ».
Astuce 1 : On remarque que toutes les fonctions ci-dessus, qui possèdent la lettre « a » dans leur nom, possèdent aussi le signe (-) juste après le tout premier terme, en effet c’est le cas des fonctions : logarithme, fractions, et des fonctions sinusoïdales (cosinus et sinus).
Cas particulier pour la fonction racine carrée, il y a deux « a », ainsi le signe (-) se trouve juste après le deuxième terme !
Astuce 2 : On remarque ensuite que pour toutes les fonctions possédant la lettre « c » dans leur nom, celles-ci possèdent aussi le chiffre 1 en tout premier terme, en effet c’est le cas des fonctions : cosinus, fractions, et racine.
Cas particulier pour la fonction exponentielle, celle-ci commence par un 1, pourtant il n’y a pas de « c » dans exponentielle, il faut donc penser au terme « etc.. » qui d’ailleurs représente bien quelque chose d’exponentiel !
Remarque : Ces deux astuces (« a : (-) » et « c : (1) ») complètent aussi les astuces logiques, comme le fait que sin(0) = 0 donc le DL de sinus commence à x, ou encore que ln(1+0) = ln(1) = 0 donc le DL du logarithme commence à x aussi.
Autre remarque :
L’astuce fonctionne aussi avec les équivalents usuels !
On remarque que pour la première ligne, on a les équivalents liés à l’exponentiel, la puissance, la racine carrée, le cosinus et le cosinus hyperbolique. Leur point commun ? Ces cinq équivalents possèdent un c dans leurs noms (ou la sonorité d’un c pour exponentiel), ainsi ils seront toujours suivis d’un (-1) pour donner un équivalent !
A l’inverse, dans la ligne du dessous qui comprend le logarithme, le sinus, le sinus hyperbolique, la tangente, et la tangente hyperbolique, aucun ne possède la lettre c dans leurs noms, il n’y a donc pas de (-1) !
- Différence entre poulpe, pieuvre et calamar - 1 novembre 2021
- Différence entre Mitose et Méiose - 1 novembre 2021
- Les races de vache : les reconnaître - 17 septembre 2019
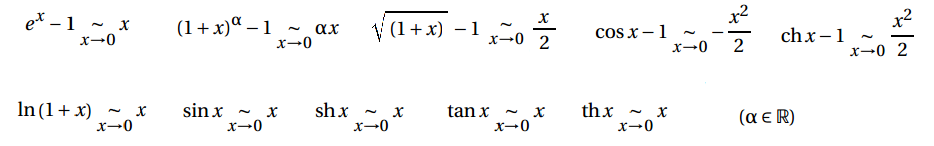
tres interessant
Complètement d’accord, d’autant que la technique du a ne fonctionne pas avec la « fraction négative ».
Il suffit de connaître les premiers termes de 1/(1-x) = 1 + x + x^2 + x^3 + …
On trouve facilement 1/(1+x) = 1 – x + x^2 – x^3 + …
On intègre pour obtenir ln(1+x) qui vaut l’intégrale de 1 – x + x^2 – x^3 + … soit ln(1+x) = x – (x^2)/2 + (x^3)/3 – (x^4)/4 + …
Pour les fonctions trigonométriques, il suffit de connaître le DL d’une d’entre-elles :
Personnellement je préfère sin x = x – (x^3)/(3!) + (x^5)/(5!) + …
On dérive et on obtient : cos x = 1 – (x^2)/(2!) + (x^4)/(4!) + …
Le DL du cosinus hyperbolique et celui du sinus hyperbolique sont respectivement le DL de cos et le DL de sin mais on remplace les « – » par des « + ».
Je préfère aussi votre méthode qu’on peut plus facilement retenir grâce au sens mathématiques que des règles sur les lettres qu’on pourrait oublier tout aussi facilement que les DL !
Et en cas de fonction dont on se souvient plus du DL, un coup de Taylor Young donne le résultat en 2 ou 3 dérivations.
Très utile