Le principe de Hardy-Weinberg peut être utilisé pour estimer la fréquence des allèles et des génotypes dans une population.
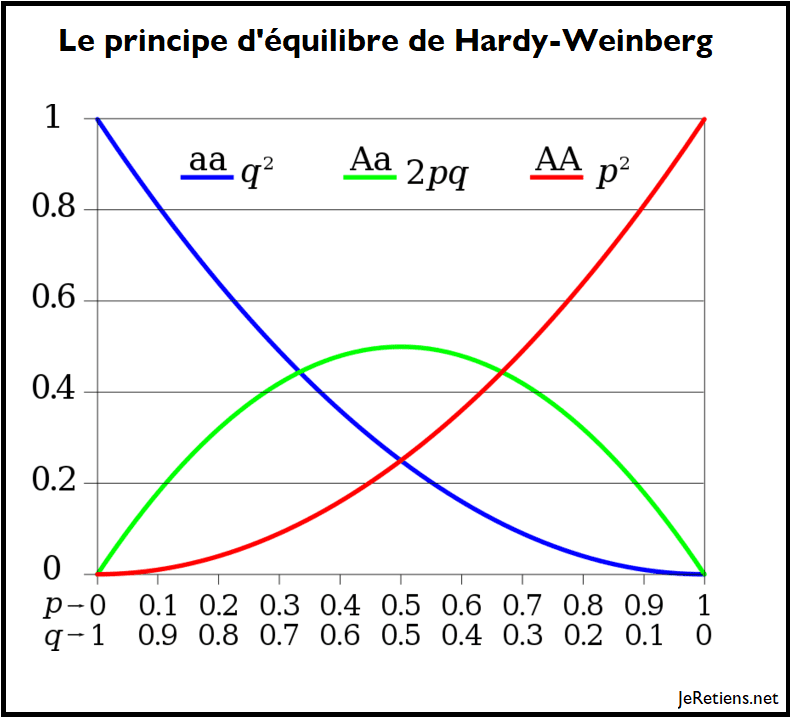
Le principe d’équilibre de Hardy-Weinberg
Le principe d’Hardy-Weinberg, loi d’Hardy-Weinberg ou encore équilibre d’Hardy-Weinberg, stipule que les fréquences des allèles et des génotypes d’une population restent constantes en l’absence de mécanismes évolutifs. Le principe de Hardy-Weinberg modélise donc une population sans évolution dans les conditions suivantes :
- pas de mutations
- pas d’immigration/émigration
- pas de sélection naturelle
- pas de sélection sexuelle
- une grande population
Bien qu’aucune population du monde réel ne puisse satisfaire à toutes ces conditions, le principe offre néanmoins un modèle utile pour l’analyse des populations.
Équations et analyse de Hardy-Weinberg
Selon le principe de Hardy-Weinberg, la variable p représente souvent la fréquence d’un allèle particulier, généralement dominant. Par exemple, supposons que p représente la fréquence de l’allèle dominant, Y, pour les cosses de pois jaunes. La variable q représente la fréquence de l’allèle récessif, y, pour les cosses de pois verts. Si p et q sont les deux seuls allèles possibles pour ce caractère, la somme des fréquences doit être égale à 1, soit 100 %. Si la fréquence de l’allèle Y dans la population est de 0,6, alors nous savons que la fréquence de l’allèle y est de 0,4.
À partir du principe de Hardy-Weinberg et des fréquences connues des allèles, nous pouvons également déduire les fréquences des génotypes. Comme chaque individu est porteur de deux allèles par gène (Y ou y), nous pouvons prédire les fréquences de ces génotypes à l’aide d’un chi carré. Si deux allèles sont tirés au hasard dans le patrimoine génétique, nous pouvons déterminer la probabilité de chaque génotype.
Dans l’exemple, nos trois possibilités de génotype sont : pp (YY), produisant des pois jaunes ; pq (Yy), également jaune ; ou qq (yy), produisant des pois verts. La fréquence des individus homozygotes pp est p2 ; la fréquence des individus hétérozygotes pq est 2pq ; et la fréquence des individus homozygotes qq est q2. Si p et q sont les deux seuls allèles possibles pour un caractère donné dans la population, la somme des fréquences de ces génotypes sera égale à un : p2 + 2pq + q2 = 1.
Dans notre exemple, les génotypes possibles sont homozygote dominant (YY), hétérozygote (Yy) et homozygote récessif (yy). Si nous ne pouvons observer que les phénotypes dans la population, alors nous ne connaissons que le phénotype récessif (yy). Par exemple, dans un jardin de 100 plants de pois, 86 peuvent avoir des pois jaunes et 16 des pois verts. Nous ne savons pas combien sont homozygotes dominants (Yy) ou hétérozygotes (Yy), mais nous savons que 16 d’entre eux sont homozygotes récessifs (yy).
Par conséquent, en connaissant le phénotype récessif et, par conséquent, la fréquence de ce génotype (16 sur 100 individus ou 0,16), nous pouvons calculer le nombre d’autres génotypes. Si q2 représente la fréquence des plantes homozygotes récessives, alors q2 = 0,16. Par conséquent, q = 0,4. Comme p + q = 1, alors 1 – 0,4 = p, et nous savons que p = 0,6. La fréquence des plantes homozygotes dominantes (p2) est de (0,6)2 = 0,36. Sur 100 individus, il y a 36 plantes homozygotes dominantes (YY). La fréquence des plantes hétérozygotes (2pq) est 2(0,6)(0,4) = 0,48. Par conséquent, 48 plantes sur 100 sont hétérozygotes jaunes (Yy).
Les applications du modèle de Hardy-Weinberg
La variation génétique des populations naturelles change constamment en raison de la génétique des populations soit la dérive génétique, les mutations, les migrations et la sélection naturelle et sexuelle. Le principe de Hardy-Weinberg donne aux scientifiques une base mathématique d’une population non évolutive à laquelle ils peuvent comparer les populations évolutives. Si les scientifiques enregistrent les fréquences des allèles au fil du temps, puis calculent les fréquences attendues sur la base des valeurs de Hardy-Weinberg, ils peuvent émettre des hypothèses sur les mécanismes à l’origine de l’évolution de la population.
Conclusion
Le principe de Hardy-Weinberg suppose que dans une population donnée, la population est grande et ne subit pas de mutation, de migration, de sélection naturelle ou de sélection sexuelle.
La fréquence des allèles dans une population peut être représentée par p + q = 1, avec p égal à la fréquence de l’allèle dominant et q égal à la fréquence de l’allèle récessif.
La fréquence des génotypes dans une population peut être représentée par p2+2pq+q2= 1, avec p2 égal à la fréquence du génotype dominant homozygote, 2pq égal à la fréquence du génotype hétérozygote, et q2 égal à la fréquence du génotype récessif.
La fréquence des allèles peut être estimée en calculant la fréquence du génotype récessif, puis en calculant la racine carrée de cette fréquence afin de déterminer la fréquence de l’allèle récessif.
- Du Soleil Invaincu au dimanche chrétien : L’héritage méconnu de Sol Invictus - 4 octobre 2024
- Les dix Plaies d’Égypte - 4 octobre 2023
- Quels étaient les impôts au Moyen Âge ? - 8 mars 2023
