L’énigme des 3 fourmis et du triangle

Des fourmis, un triangle, et une simple question de probabilités !

Énoncé

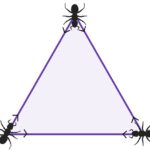
Trois fourmis se trouvent aux trois coins d’un triangle équilatéral. Chaque fourmi choisit au hasard une direction et commence à se déplacer le long du bord du triangle.
Quelle est la probabilité qu’aucune des fourmis n’entre en collision ?

Un indice ?

Cette question est bien plus facile qu’elle n’en a l’air. Comme pour la plupart de ces types de questions, nous devons réfléchir aux configurations possibles !
Chacune des trois fourmis peut se déplacer dans 2 directions. Ce qui veut dire qu’il y a 2+2+2 configurations auxquelles s’ajoute le fait que les fourmis peuvent tourner dans le sens des aiguilles d’une montre ou dans le sens inverse. Cela fait donc 2+2+2+2 possibilités. Mais combien d’entre elles répondent au critère de l’absence de collisions ?

Solution

Pour qu’il n’y ait pas de collision, il faut que toutes les fourmis se déplacent dans la même direction. Tous dans le sens des aiguilles d’une montre ou tous dans le sens inverse.

Supposons donc que les fourmis ont 50% de chances de choisir l’une ou l’autre direction. La probabilité qu’elles décident toutes d’aller dans le sens des aiguilles d’une montre est donc donnée par ½ ½ ½ ½ = 0,125

La probabilité qu’elles décident toutes d’aller dans le sens inverse des aiguilles d’une montre est donnée par ½ ½ ½ ½ = 0,125

L’une ou l’autre de ces méthodes nous permettra de faire la somme des probabilités qui nous donne 0,25 soit 25%.

Il y a une autre approche qui permet de résoudre le problème et qui nécessite moins de compréhension des probabilités. C’est la méthode qui découle de l’indice !
Reprenons en détails: avec trois fourmis ayant chacune deux choix, nous avons 2+2+2+2 = 8 configurations possibles. Si A indique le sens antihoraire et C le sens horaire, les configurations sont AAA, AAC, ACA, ACC, CAA, CAA, CAC, CCA & CCC. Sur ces 8, 2 seulement nous sont utiles. AAA et CCC. 2 sur 8 équivalent à ¼ ou 0,25, soit 25% !