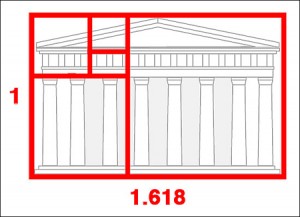
Le nombre d’or, noté φ est est la solution positive de l’équation x² – x – 1 = 0, soit (1 + √5) / 2.
Le nombre d’or est irrationnel dont voici les premières décimales: 1,61803398…
Il s’agit d’un rapport numérateur sur dénominateur, donc d’une proportion.
Ce nombre tient sa perfection d’une propriété particulière; il représente l’unique proportion a/b entre deux longueurs où le rapport entre la somme de a (la plus grande des longueurs) et de b (la plus petite des longueurs) sera égale au rapport de la plus grande des longueurs a sur la plus petite b.
Autrement dit: (a + b)/a = a/b.
Cette proportion est considérée comme parfaite par les architectes depuis l’antiquité et de nombreux monuments ont été construits en respectant ce nombre.
La perfection architecturale était d’avoir un bâtiment rectangulaire d’une largeur d’une unité et d’une longueur de φ unité.
Pour se souvenir du nombre d’or, il suffit de retenir la phrase suivante « Ô nombre d‘élégance ! Toi, toi, grandiose, étonnant« .
Le nombre de lettres de chaque mot correspond à un chiffre du nombre d’or. Le point d’exclamation marque le 0.
Pour: 1,61803398.
- Hallucinations d’IA – Quand les robots rêvent - 19 août 2025
- Pourquoi coopérer ? Le dilemme du prisonnier à l’épreuve de l’évolution - 1 août 2025
- Machine learning, quand l’IA regarde les nuages - 29 juillet 2025
Rejoignez-nous sur Instagram !
Découvrez nos infographies et astuces : @JeRetiensNet

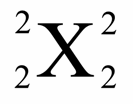
ca cartonne ce truc