Carré des nombres de 2 chiffres

par

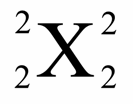
x_carréDe la relation (a+b) x (a+b) = a²+ 2ab+b² nous tirons une règle similaire pour calculer le carré d’un nombre de 2 chiffres.

Soit à calculer le carré de 53 (c’est-à-dire 53×53), nous procédons de la droite vers la gauche comme dans une multiplication normale, nous avons:

b² = 3×3 = 9 c’est le chiffre le plus à droite du résultat, puis :

2ab = 2x(5×3) = 30, nous avons le zéro comme chiffre à conserver et 3 en retenue.

a² = 5×5 = 25 + nos 3 de retenue qui font 28.

Nous avons le résultat de 53 au carré : 28-0-9, soit 2809.

Rassurez-vous c’est en fait plus difficile à expliquer qu’à calculer.
Une méthode plus simple serait de décomposer le nombre en une somme de nombres/chiffres dont les carrés sont connus et simples.
Par exemple pour 46:
(46)² = (40 + 6)² = 40² + 2*40*6 + 6*6 = 1600 + 480 + 36 = 2116

Par Thierry Martin (53) et Dimitra Melanitis (explication simplifiée et 46)

Dimitra Melanitis
Les derniers articles par Dimitra Melanitis (tout voir)

5 réflexions au sujet de “Carré des nombres de 2 chiffres”

  3. Une méthode plus simple serait de décomposer le nombre en une somme de nombres/chiffres dont les carrés sont connus et simples.
    Par exemple pour 46:
    (46)² = (40 + 6)² = 40² + 2*40*6 + 6*6 = 1600 + 480 + 36 = 2116

    Répondre

  4. On commence par le chiffre des unités (6 ici)
    6*6 = 36
    On va reporter le chiffre des dizaines 3 du nombre 36 obtenu au calcul suivant:
    2*4*6 = 48, nombre auquel on ajoute le report ci-dessus, c'est-à-dire 3. Cela nous donne 51. On va à nouveau reporter le chiffre des dizaines, 5, de ce résultat au calcul suivant:
    4*4 = 16, nombre auquel on ajoute le report ci-dessus 16+5 = 21.
    En commençant par le bas, on met côte à côte les résultats:
    21 suivi de 1 (nous avions utilisé le 5 de 51 comme report, il nous restait le 1 à utiliser) suivi de 6 (nous avions utilisé le chiffre 1 comme report)
    Ce qui nous donne 46*46 = 2116

    Répondre

Laisser un commentaire