Connaissez-vous les comportements aux limites d’une bobine et d’un condensateur ?
Tout d’abord, en électricité, tout se démontre à l’aide de calculs, mais cela peut prendre du temps précieux, il est donc important de connaître immédiatement des résultats.
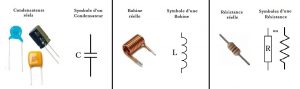
Avant d’aborder les explications, puis les astuces, il faut déjà savoir représenter un condensateur et une bobine !
Comme le montre l’illustration, une bobine est représentée par un L, le condensateur par un C et la résistance par un R.
– Un Condensateur est un composant électronique constitué de deux armatures conductrices (électrodes), séparées par un isolant polarisable (ou diélectrique).
La propriété principale du condensateur est de pouvoir stocker des charges électriques opposées sur ses deux armatures ; ainsi le condensateur peut stocker de l’énergie.
Dans la vie de tous les jours, les condensateurs sont utilisés pour éviter les sauts de tension dans les appareils, en effet les condensateurs peuvent se charger et se décharger, ils peuvent aussi avoir un rôle dans les filtrages.
– Une bobine (solénoïde) est un composant en électronique, constitué d’un enroulement de fil conducteur.
Les bobines sont utilisées pour créer une impulsion de haute tension (moteur électrique), ou lorsqu’on l’associe avec d’autres composants, elle permet de filtrer (amplificateurs audio ou enceintes).
Après cette description générale, il faut maintenant voir les unités qui vont entrer en jeu :
- L’unité de la bobine est le Henry (H) souvent en mH (millihenry).
- L’unité du condensateur est le Farad (F) souvent en µF (microfarad).
- L’unité d’une résistance est le Ohm (Ω, oméga) souvent en kΩ (kiloohm).
- On sait que la période T (en seconde) est égale à 2π sur la pulsation ω (oméga) (en radians par seconde), soit T = 2π/ω.
- On sait que la fréquence f (en Hertz) est égale à l’inverse de la période T, soit f = 1/T.
En reliant ces deux dernières équations, on obtient f = ω/2π (l’inverse de T), ainsi la pulsation ω est proportionnelle à la fréquence f, puisque quand la pulsation ω augmente, la fréquence f augmente elle aussi, ce qui va nous être utile pour la suite.
On s’intéresse maintenant aux deux composants les plus utilisés en électricité : la Bobine (L) et le Condensateur (C)
À très basse fréquence (TBF : c’est-à-dire lorsque la pulsation ω (oméga) est presque nulle, soit proche de 0), une bobine L (idéale) se comporte comme un fil (c’est-à-dire un interrupteur fermé).
À l’inverse, cette bobine idéale se comporte comme un interrupteur ouvert à très haute fréquence (THF : c’est-à-dire lorsque la pulsation ω diverge vers + l’infini).
C’est le contraire avec un condensateur, celui-ci se comporte comme un interrupteur ouvert à TBF et comme un fil à THF.
Toutefois, on peut facilement se tromper, en inversant bobine L et condensateur C, alors comment faire pour ne pas confondre le comportement de ces deux composants ?
L’astuce : à très basse fréquence (TBF), la pulsation ω (oméga) diminue pour se rapprocher de 0, il faut donc imaginer qu’on aplatisse la bobine, c’est-à-dire qu’il faut imaginer que la bobine (idéale) s’amenuise jusqu’à avoir l’épaisseur d’un fil.
Ainsi, à partir de cette astuce, on retrouve les quatre cas ! (En effet, si à TBF : bobine = fil (= interrupteur fermé), alors le condensateur = interrupteur ouvert ; inversement, à THF : bobine = interrupteur ouvert, alors condensateur = fil).
- Différence entre poulpe, pieuvre et calamar - 1 novembre 2021
- Différence entre Mitose et Méiose - 1 novembre 2021
- Les races de vache : les reconnaître - 17 septembre 2019
){kind=link}
Merci pour le moyen mnémotechnique
Très bonne thématique mais j’aimerais bien avoir une démonstration