Le paradoxe de Condorcet, l’un des concepts les plus fascinants de la théorie du choix social, interroge la logique des systèmes de vote. Il démontre comment des préférences individuelles, pourtant cohérentes, peuvent aboutir à des cycles d’irrationalité collective. Ce phénomène soulève des questions essentielles sur la démocratie, l’équité et la légitimité des processus décisionnels.
L’actualité et la pertinence de ce paradoxe dans les débats sur la réforme des systèmes électoraux et l’optimisation des processus de décision en entreprise en font un sujet incontournable. Dans cet article, nous analysons le paradoxe de Condorcet sous ses aspects historiques, mathématiques et pratiques afin d’offrir une vision complète et nuancée de ce phénomène.
En bref : le paradoxe de Condorcet
- Le paradoxe de Condorcet est un phénomène où des préférences individuelles logiques entraînent une préférence collective illogique.
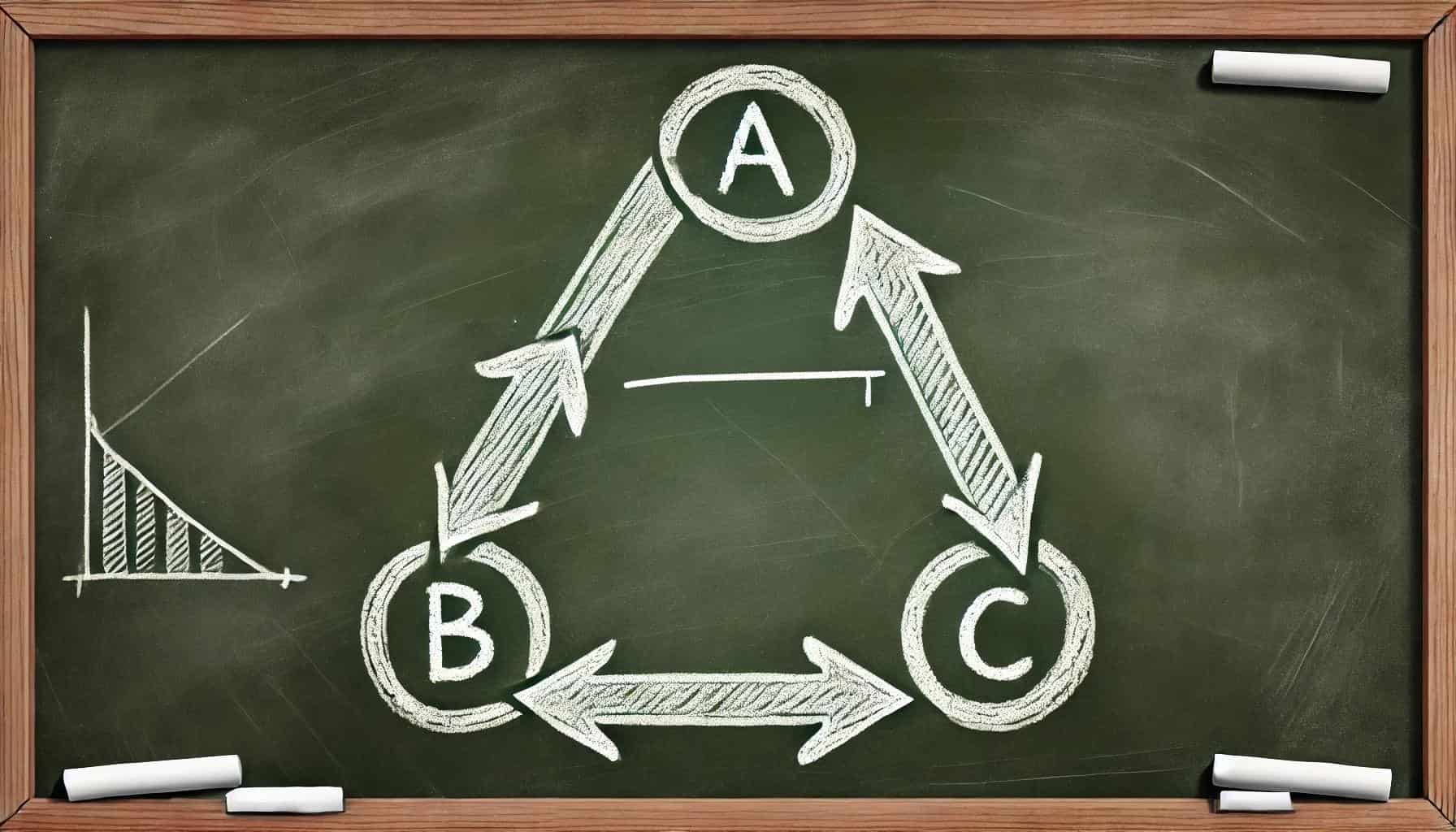
- Il se manifeste par des cycles de préférence, comme A > B, B > C, et C > A, où aucun candidat n’est majoritaire.
- Ce paradoxe remet en question la légitimité des systèmes de vote basés sur la majorité simple.
- Il a des implications importantes pour la théorie du choix social et les systèmes électoraux.
- Il a poussé à la création de systèmes de vote alternatifs pour éviter ces impasses.
Introduction
Le paradoxe de Condorcet, nommé d’après le philosophe, mathématicien et homme politique Nicolas de Condorcet (1743-1794), soulève une question essentielle : peut-on réellement agréger des préférences individuelles en une décision collective cohérente ? Dans cet article, nous examinerons d’abord les origines historiques et conceptuelles du paradoxe, avant de détailler ses mécanismes et de proposer des exemples concrets illustrant les limites des systèmes électoraux traditionnels. Nous aborderons ensuite les implications théoriques et pratiques de ce paradoxe, en mettant en lumière aussi bien ses applications contemporaines que ses critiques. Nous verrons ainsi comment, malgré sa complexité, le paradoxe de Condorcet offre des perspectives d’amélioration pour nos systèmes de gouvernance et de choix en général.
Origines historiques et conceptuelles du paradoxe de Condorcet
Le concept du paradoxe de Condorcet trouve son origine dans les travaux de Nicolas de Condorcet (1743-1794), dont les recherches sur la probabilité, la logique et la politique ont profondément marqué la pensée démocratique. Condorcet s’intéressait à la manière dont une société peut, en agrégeant les préférences individuelles, parvenir à un choix collectif représentant fidèlement la volonté du plus grand nombre. Il en est venu à constater que, dans certaines conditions, la somme des préférences individuelles pouvait être irrationnelle et même conduire à des cycles de décision, ce qui constitue le cœur du paradoxe.
Les fondements théoriques reposent sur l’idée que même si chaque électeur a une préférence rationnelle entre deux options, l’agrégation de ces préférences peut produire un résultat intransitif. Par exemple, dans un scrutin à trois candidats, il est possible d’avoir une majorité préférant le candidat A à B, une autre majorité préférant B à C, et une troisième majorité préférant C à A. Ce phénomène montre que la démocratie majoritaire peut, en apparence, manquer de cohérence logique et soulever des interrogations sur la validité de certains systèmes électoraux.
Les fondements mathématiques
Les travaux de Condorcet ont inauguré une réflexion mathématique sur l’agrégation des préférences. La théorie du choix social s’appuie sur des modèles mathématiques afin de démontrer que, sous certaines conditions, aucun système de vote ne peut satisfaire simultanément plusieurs critères de rationalité et d’équité. Le paradoxe illustre cette impossibilité en prouvant que, même dans une situation où chaque votant évalue logiquement ses choix, l’ensemble des préférences peut se révéler cyclique.
Mécanismes et exemples concrets
Pour comprendre le paradoxe de Condorcet, il est essentiel d’illustrer ses mécanismes par des exemples concrets et pratiques. Dans de nombreux systèmes de vote, notamment ceux basés sur la majorité simple, le paradoxe se manifeste à travers l’apparition de cycles de préférence.
Exemple pratique : l’élection à trois candidats
Imaginons une élection opposant trois candidats : A, B et C. Supposons que les électeurs aient les préférences suivantes :
- Un groupe majoritaire préfère A à B,
- Un autre groupe majoritaire préfère B à C,
- Un troisième groupe majoritaire préfère C à A.
Il en résulte que, lors d’un vote majoritaire, chaque candidat peut battre un autre, mais aucun n’émerge clairement comme gagnant global. Ce cycle de préférence—A bat B, B bat C, et C bat A—illustre parfaitement le paradoxe de Condorcet. Dans ce cas, le système de vote semble contredire la logique collective en produisant un résultat intransitif, malgré la rationalité individuelle des choix.
Lien avec la théorie du choix social
Le paradoxe de Condorcet trouve une résonance particulière dans la théorie du choix social, qui étudie comment les préférences individuelles peuvent être agrégées pour former une décision collective. Des théoriciens contemporains, comme Kenneth Arrow (1921-2017), ont montré, par le biais du célèbre théorème d’impossibilité, qu’aucun système de vote ne peut concilier de manière parfaite des critères d’universalité, de non-dictature, de Pareto-efficience et d’indépendance des alternatives. Le paradoxe de Condorcet en est une illustration concrète, mettant en avant les tensions entre ces critères essentiels dans la prise de décision collective.
Implications et critiques du paradoxe de Condorcet
Le paradoxe de Condorcet ne se limite pas à une curiosité théorique ; il possède des implications réelles pour les systèmes électoraux et la démocratie représentative. Son existence soulève d’importantes questions sur la légitimité et l’efficacité des méthodes de vote.
Conséquences pour les systèmes électoraux
En confrontant le paradoxe de Condorcet, de nombreux systèmes électoraux se trouvent en difficulté pour déterminer un gagnant clair lors d’élections comportant plusieurs candidats. Le phénomène montre qu’il peut être dangereux de se reposer uniquement sur la simple majorité pour agréger les préférences individuelles. Dans certains cas, des mécanismes alternatifs, comme le scrutin à second tour ou des systèmes de vote préférentiel, ont été proposés pour contourner les limitations mises en évidence par le paradoxe.
Limites de l’approche de Condorcet
Toutefois, il convient de nuancer l’enthousiasme suscité par la reconnaissance du paradoxe. Si celui-ci expose des failles dans les systèmes de vote traditionnels, l’approche de Condorcet n’est pas exempte de critiques. Certains analystes soulignent que la fréquence des situations conduisant à des cycles de préférence reste relativement faible dans des contextes réels. De plus, des ajustements méthodologiques et l’emploi de systèmes combinés peuvent contribuer à atténuer l’impact de ce paradoxe sur la prise de décision collective.
Perspectives contemporaines et applications
Le paradoxe de Condorcet continue d’intéresser les chercheurs et les praticiens dans divers domaines, allant de la science politique à l’informatique en passant par l’économie. Son étude a conduit à des avancées dans la conception d’algorithmes de décision et de systèmes de vote en ligne, favorisant une meilleure compréhension de la dynamique collective.
Innovations dans les systèmes de vote
Face aux défis posés par le paradoxe, plusieurs initiatives se sont orientées vers la création de systèmes de vote hybrides. Ces systèmes combinent différents modes de scrutin pour tenter d’éviter les cycles de préférence. Par exemple, l’utilisation d’un vote par approbation ou d’un vote à classement permet de recueillir des informations plus détaillées sur les préférences individuelles, contribuant ainsi à une meilleure agrégation des opinions.
Applications dans la prise de décision algorithmique
Dans le domaine de l’intelligence artificielle et de la prise de décision algorithmique, le paradoxe de Condorcet offre des enseignements précieux. Les chercheurs s’appuient sur des modèles inspirés de ce paradoxe pour concevoir des algorithmes capables d’anticiper et de résoudre les conflits d’intérêts entre des choix multiples. Par exemple, dans les systèmes de recommandation ou dans les processus de gouvernance numérique, la capacité à détecter et à contourner les cycles de préférence peut se révéler déterminante pour garantir une prise de décision efficace et équitable.
Réflexions sur l’évolution de la démocratie
L’analyse du paradoxe de Condorcet soulève également des questions fondamentales sur l’évolution de la démocratie. À l’ère des réseaux sociaux et de la communication instantanée, la pluralité des opinions et la diversité des sources d’information contribuent à rendre le processus de décision collective encore plus complexe. Le paradoxe nous rappelle l’importance de concevoir des mécanismes inclusifs et résilients, capables de s’adapter aux transformations rapides de notre société.
Conclusion
En somme, l’exploration du paradoxe de Condorcet nous conduit à plusieurs constats majeurs. D’une part, il met en lumière les failles potentielles du système de vote majoritaire en révélant comment des préférences individuelles, pourtant rationnelles, peuvent se transformer en choix collectifs incohérents. D’autre part, il souligne la nécessité de repenser les mécanismes d’agrégation des opinions en s’appuyant sur une approche multidimensionnelle qui intègre à la fois des éléments historiques, mathématiques et pratiques.
L’analyse du paradoxe de Condorcet rappelle que la simple application d’une majorité ne suffit pas toujours à garantir des décisions justes et représentatives. Le paradoxe offre un cadre stimulant pour interroger la nature du processus démocratique et pour envisager des alternatives plus robustes et innovantes. Ce questionnement est d’autant plus crucial à une époque où la complexification des enjeux sociaux et technologiques appelle à une refonte continue des méthodes de gouvernance. L’enjeu est de trouver le juste équilibre entre la représentation fidèle des préférences individuelles et l’obtention de résultats cohérents et durables pour la société dans son ensemble.
FAQ : Le paradoxe de Condorcet
Qui était Nicolas de Condorcet ?
Nicolas de Condorcet (1743-1794) était un philosophe, mathématicien et homme politique français. Il est connu pour ses travaux sur le vote et la démocratie, et a été le premier à identifier le paradoxe qui porte aujourd’hui son nom.
Qu’est-ce que le paradoxe de Condorcet en termes simples ?
C’est un phénomène où la volonté du peuple, exprimée par des préférences individuelles, peut devenir incohérente au niveau collectif. Par exemple, un groupe de personnes peut préférer A à B, B à C, mais aussi C à A. Il n’y a pas de gagnant clair, ce qui est paradoxal.
Comment se manifeste un cycle de préférence ?
Un cycle de préférence se produit lorsque, dans un scrutin à trois candidats ou plus, il n’y a pas de vainqueur majoritaire. Chaque candidat peut battre un autre, mais aucun ne peut les battre tous. On parle d’un cycle intransitif : A > B, B > C, et C > A.
Le paradoxe de Condorcet est-il fréquent ?
Des études théoriques montrent que ce paradoxe est peu fréquent dans des contextes électoraux réels avec un grand nombre d’électeurs. Cependant, il peut se produire dans des situations spécifiques, notamment avec un petit nombre de votants et de candidats, ou si les préférences sont très polarisées.
Quel est le lien entre le paradoxe de Condorcet et la théorie du choix social ?
Le paradoxe de Condorcet est un exemple concret et précoce des problèmes étudiés par la théorie du choix social. Le célèbre théorème d’impossibilité d’Arrow s’inscrit directement dans cette lignée de recherche en montrant qu’il est impossible de créer un système de vote idéal qui satisfasse tous les critères d’équité.
Comment peut-on éviter le paradoxe de Condorcet ?
Le paradoxe peut être évité en utilisant des systèmes de vote alternatifs au scrutin majoritaire simple, tels que le scrutin à second tour, le vote par approbation, ou des méthodes de classement qui prennent en compte l’ensemble des préférences des électeurs.
Quel est le système de vote de Condorcet ?
Le système de vote de Condorcet est une méthode qui consiste à confronter chaque candidat à tous les autres, en tête-à-tête. Le vainqueur de Condorcet est le candidat qui bat tous les autres. Le paradoxe de Condorcet se produit lorsque, justement, aucun vainqueur n’émerge.
Le paradoxe de Condorcet a-t-il des implications pour la démocratie ?
Oui, il interroge la légitimité des décisions collectives, surtout lorsqu’elles sont prises par une majorité simple. Le paradoxe montre que la « volonté du peuple » peut être une notion complexe, voire incohérente, et qu’il faut en tenir compte pour concevoir des systèmes de vote plus robustes.
Qu’est-ce que l’intransitivité ?
L’intransitivité est une relation mathématique où, si l’on a A > B et B > C, on n’a pas nécessairement A > C. C’est le principe qui est au cœur du paradoxe de Condorcet, où les préférences collectives ne suivent pas une logique transitive.
Quel est l’apport du paradoxe à la science politique ?
Le paradoxe a forcé les chercheurs en science politique à examiner les faiblesses des systèmes de vote majoritaire. Il a stimulé la recherche sur la conception des systèmes électoraux et la manière dont les préférences individuelles sont agrégées pour aboutir à une décision collective.
Le paradoxe de Condorcet est-il lié au théorème d’Arrow ?
Oui, le théorème d’Arrow est une généralisation plus formelle du problème soulevé par le paradoxe de Condorcet. Il démontre qu’aucun système de vote ne peut être considéré comme parfait, car il est impossible de satisfaire plusieurs critères de rationalité en même temps.
Le paradoxe a-t-il des applications en dehors de la politique ?
Oui, le paradoxe de Condorcet s’applique à toute situation de choix collectif, comme les décisions en entreprise, les recommandations algorithmiques ou les systèmes de classement. Il aide à comprendre comment des préférences individuelles peuvent créer des conflits d’intérêts et des impasses.
- Comment, au snooker, un joueur prévoit sa position plusieurs coups à l’avance - 19 janvier 2026
- Depuis quand fête-t-on le Nouvel An le 1er janvier ? - 31 décembre 2025
- Les heures canoniales: matines, laudes, prime, tierce, sexte, none, vêpres, complies - 18 décembre 2025
Rejoignez-nous sur Instagram !
Découvrez nos infographies et astuces : @JeRetiensNet


