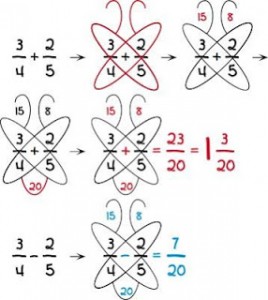
« On ne mélange pas les pommes et les poires » nous ont répété sans relâche nos instituteurs.
La théorie de cette opération veut que l’on trouve le dénominateur commun. La façon la plus simple de faire cela est de multiplier les deux dénominateurs. Dans le dessin, ici, 4 et 5. Cela nous donne 20 comme dénominateur commun. (1)
Cela étant fait, il faut que les fractions restent en proportions identiques. Si on a multiplié le 4 de 3/4 par 5, il faut aussi multiplier le 3 de 3/4 par 5. De même, on a multiplié le 5 de 2/5 par 4, il faut aussi multiplier le 2 de 2/5 par 4. (2)
On obtient ainsi deux nouvelles fractions à additionner: 15/20 + 8/20. Et nous avons presque terminé! Maintenant que nous n’avons plus que des pommes, ou plus que des poires, nous pouvons en additionner les quartiers! Le résultat est 23/20. Nous pouvons aller plus loin en considérant que 23/20 = 20/20 + 3/20 c’est-à-dire 1+3/20.
La soustraction fonctionne de la même façon.
Ce moyen mnémotechnique permet de retrouver ces étapes de calcul à travers le dessin d’un papillon. Les ailes représentent les multiplications croisées décrites en (2). Dans les antennes du papillon, on écrit le résultat de ces multiplications pour le numérateur. Le postérieur du papillon représentera le dénominateur commun, trouvé via la méthode (1).
Il ne reste plus qu’à additionner les antennes et les diviser par le postérieur du papillon. Facile, non?
Consultante chez melan-IT
Dimitra Melanitis est une professionnelle de l'informatique et consultante chez melan-IT, forte de plus d'une décennie d'expérience en ingénierie logicielle, analyse fonctionnelle et conception de systèmes. Ayant travaillé principalement dans un cadre scientifique, elle excelle à structurer la complexité et à créer des solutions pragmatiques. Son amour profond pour les livres, allié à sa rigueur et sa quête de clarté, l'amène à décrypter et rendre accessibles les sujets techniques les plus ardus, comme le machine learning et ses applications en météorologie.
Les derniers articles par Dimitra Melanitis (tout voir)
- Hallucinations d’IA – Quand les robots rêvent - 19 août 2025
- Pourquoi coopérer ? Le dilemme du prisonnier à l’épreuve de l’évolution - 1 août 2025
- Machine learning, quand l’IA regarde les nuages - 29 juillet 2025
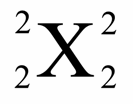
mutiplication papillon, multiplication sans problème en on (desolee je n’ai pas trouve mieux mais c’est super comme truc)